コードカキタイ
プログラミング
Python
Pythonでの行列演算にはNumPyが便利！行列の基礎と活用法を解説

Python

最終更新日: 2022.12.23 (公開: 2022.12.23)

Pythonでの行列演算にはNumPyが便利！行列の基礎と活用法を解説

Pythonでは、縦方向と横方向の値の並びから成る「行列」を計算できます。Pythonは、データや数値の解析に活用されることが多いこともあり、行列演算が得意なプログラミング言語です。行列演算を活用すると、多種・多量の数値を効率的に計算したり、画像データを数学的に処理したりすることができます。

しかし、Pythonの標準的な「リスト」を使うと、ソースコードが冗長・複雑になるので分かりにくく、思わぬミスにつながってしまうことがあります。そこで便利なのが、数値計算を効率的に行うためのライブラリ「NumPy」です。NumPyを使えば、高度な行列演算を簡単に行うことができます。そこで本記事では、Pythonの行列演算をNumPyで行う方法や、応用テクニックを紹介します。

そもそも「行列」とは？縦横に値を配列したもの
Pythonの「リスト」で行列を扱う方法
Pythonの「NumPy」ライブラリを使えば行列演算が簡単に！
PythonのNumPyの基本的な関数と使い方
NumPyでさまざまな行列演算を試してみよう！
【応用編】NumPyで画像データも扱える！
- Pillow（PIL）をVisual Studioにインストールする方法
【応用編】Pillow（PIL）の基本的な使い方
【実践編】NumPyの画像処理テクニック9選！
PythonでNumPyを活用して行列を便利に操作しよう！

そもそも「行列」とは？縦横に値を配列したもの

そもそも「行列（Matrix）」とは、縦と横に値を配列したものです。横方向に並んだ「行」と縦方向に並んだ「列」から成り、各要素の数によってさまざまな種類に分けられます。

たとえば上記の行列は、横方向の配列が2組、縦方向の配列が3組あるため、「2×3型」の行列と呼ばれます。配列された要素は行列の「成分」と呼ばれ、行列の第i行目・第j列目の成分を「(i, j) 成分」と表します。

行列は通常の値「スカラー」とは異なり、「ベクトル」と呼ばれる特殊な概念のひとつです。行列にも「足し算」や「掛け算」などの演算がありますが、その演算方法はスカラーとは異なります。この行列が活用されるのは、主にデータや数値の解析、画像やグラフィックスの処理などの分野です。たとえば3Dゲームのプログラミングでは、オブジェクトを表示するために行列演算を行って、スクリーンのどこに表示するかを計算しています。

Pythonは分析・解析の分野での導入実績が豊富ですが、それはPythonが行列演算に長けたプログラミング言語だからです。まずは、Pythonで行列を扱う方法について確認していきましょう。

Pythonの「リスト」で行列を扱う方法

Pythonの標準機能で行列を扱うためには、「リスト」を使うのが一般的です。たとえば、2×2型の行列を生成・表示するプログラムは以下のとおりです。

//サンプルプログラム

# 2×2型の行列を生成する
matrix = [
  [1, 2],
  [3, 4],
]

# フォーマット機能を使用して行列を表示する
print("行列：{}".format(matrix))

//実行結果

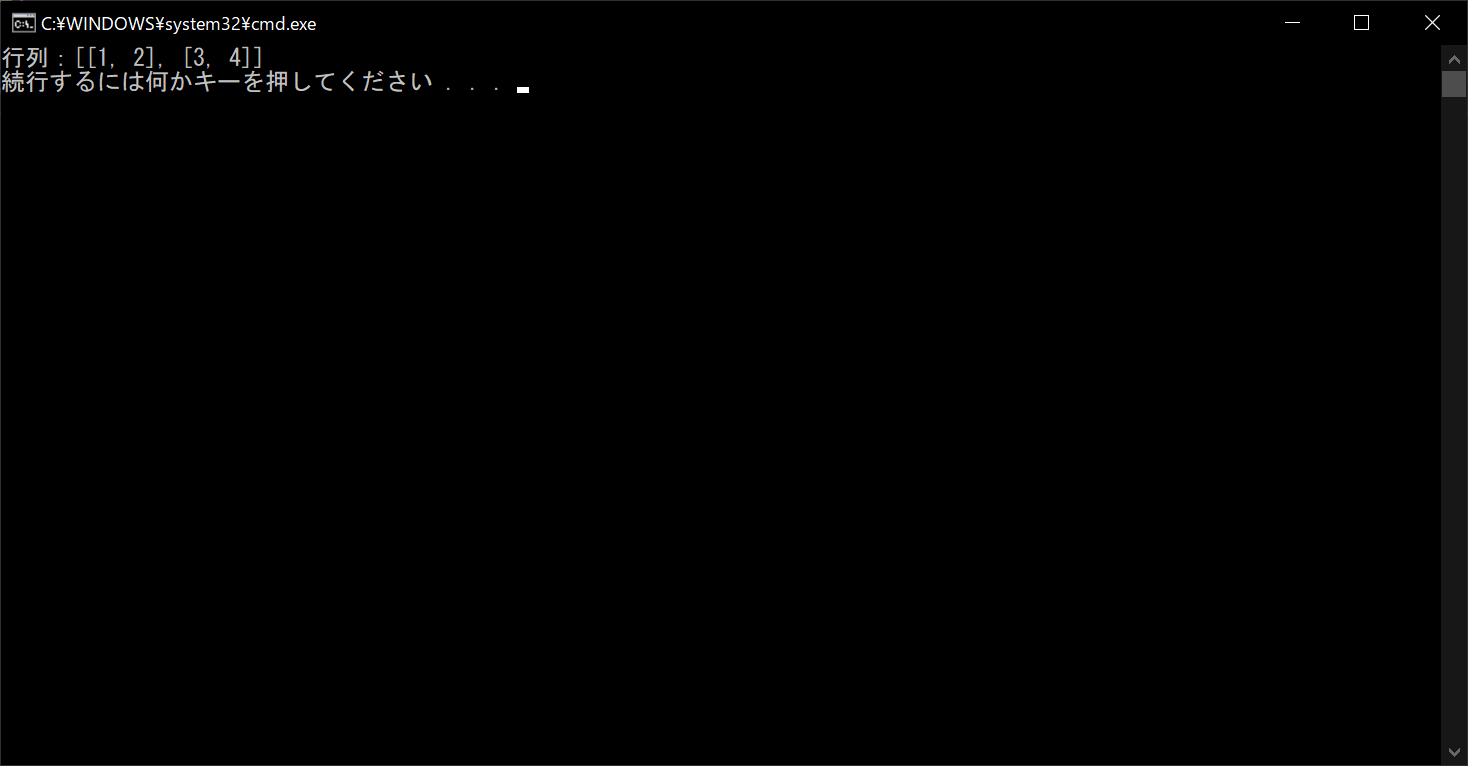
行列演算で頻繁に登場する「転置行列」は、以下のサンプルコードのように記載すると作れます。

//サンプルプログラム

# 2×2型の行列を生成する
matrix = [
  [1, 2],
  [3, 4],
]

# 転置行列を計算する
transpose = list(zip(*matrix))

# フォーマット機能を使用して行列を表示する
print("行列：{}".format(transpose))

//実行結果

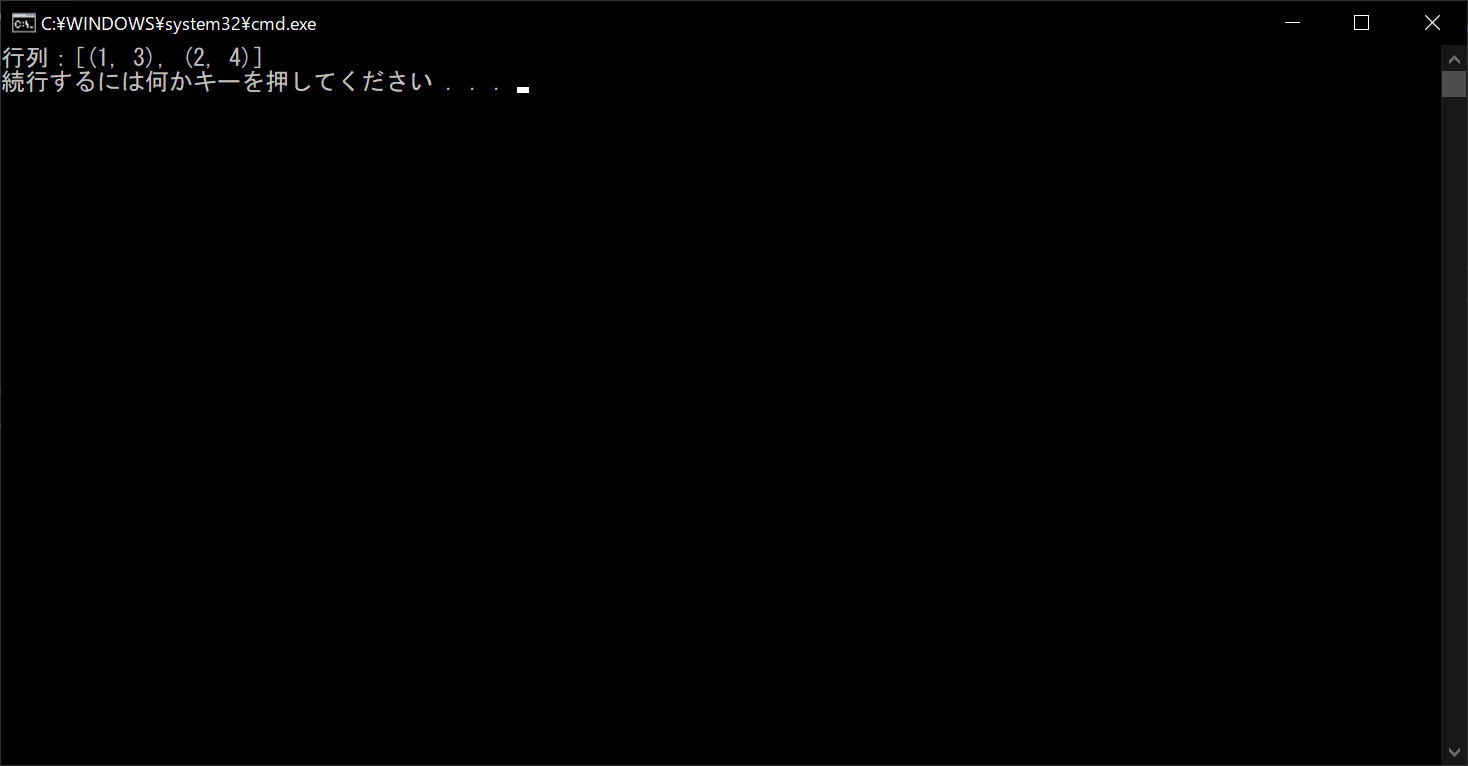
zip関数には、複数のデータをまとめる機能があり、多次元配列に対して使うと配列データを加工できます。ただし、データをまとめる方向を変えるために、行列変数の前に「*（アスタリスク）」を付ける必要があります。2つの行列の積を求めるプログラムは以下のとおりです。

//サンプルプログラム

# 2×2型の行列を2つ生成する
matrixA = [[1, 2], [3, 4]]
matrixB = [[5, 6], [7, 8]]
 
# 演算結果を格納するためのリストを用意する
result = []

# 2つの行列の積（matrixA * matrixB）を計算する
for k, v in matrixA:
  temp = []

  for kk, vv in zip(*matrixB):
    temp.append(k * kk + v * vv)

  result.append(temp)

# 演算結果行列を表示する
print(result)

//実行結果

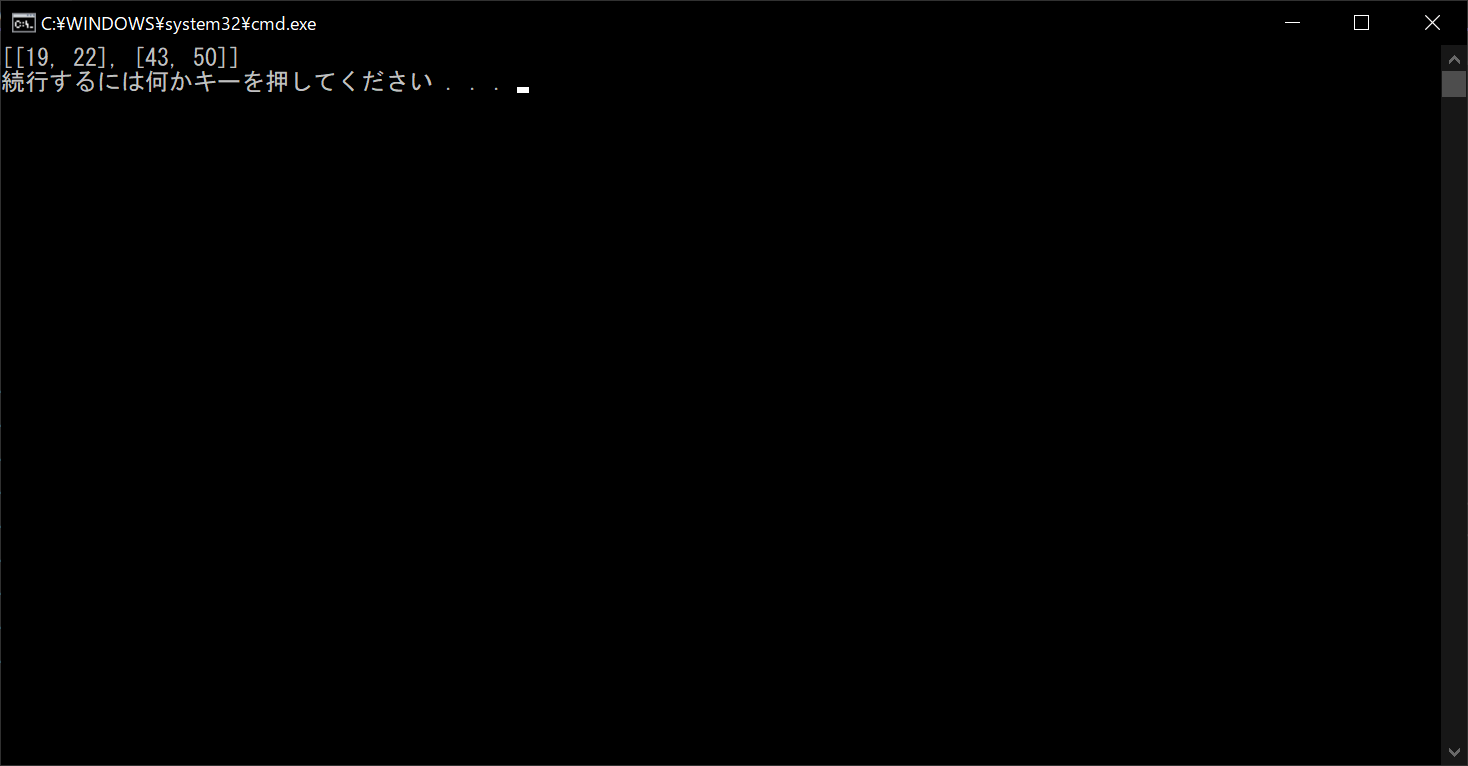
行列の積は、「Aの第m行の各成分とBの第n列の各成分の積」の和を求めることで算出できます。しかし、そのままではプログラムを組みにくいので、2つ目の行列の転置行列を求め、行同士の成分を計算できるようにしています。

いずれにせよ、行列の積を求めるプログラムには複雑な部分があるため、通常のリストで扱うのは避けたいところでしょう。

Pythonの「NumPy」ライブラリを使えば行列演算が簡単に！

前述したように、Python標準機能のリストを使えば、転置行列や積の演算などができます。しかし、演算のアルゴリズムはすべて自分で書かないといけないため、行列演算の知識がなければ使えないうえ、思わぬミスにつながってしまうこともあります。

そこで広く活用されているのが、Pythonの数値計算ライブラリ「NumPy」です。NumPyを使えば、用意されている関数を組み合わせるだけで行列演算ができるので、プログラミングの効率性と正確性を大幅に高められます。さらに、NumPyは演算速度が速いので、大量のデータを扱うときはとくにNumPyがおすすめです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で行列を生成する
matrix = numpy.array([[1, 2], [3, 4]])

# 行列の中身を画面上に表示する
print(matrix)

//実行結果

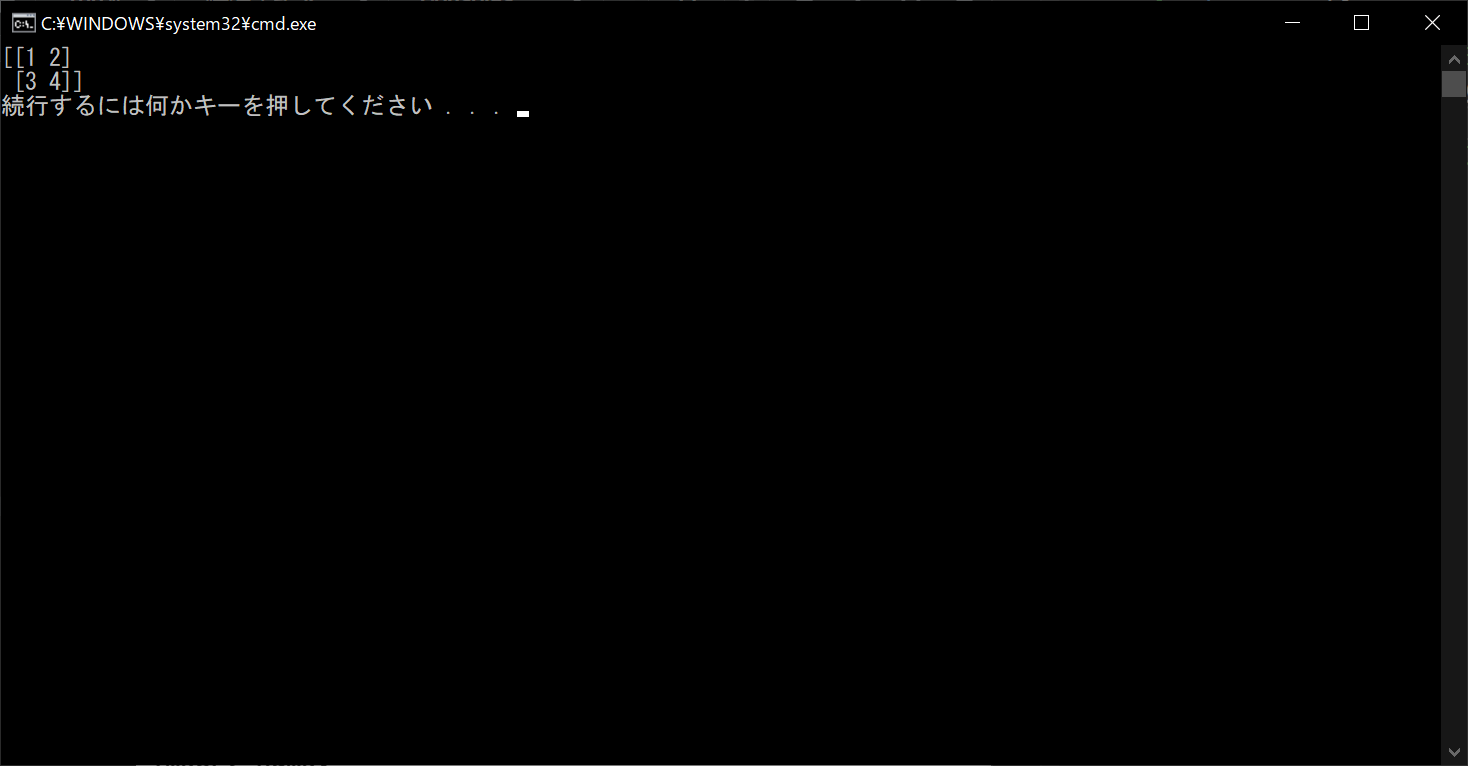
NumPyでの行列作成の手順は、以上のとおりです。NumPyライブラリをインポートして、「numpy.array関数」の引数に、行列形式で要素を指定すれば、簡単に行列変数を作成できます。画面上に中身を表示するときは、「print関数」に行列変数をそのまま渡すだけです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で行列を生成する
matrix = numpy.array([[1, 2], [3, 4]])

# 転置行列を取得する
transpose = matrix.T

# 転置行列の中身を画面上に表示する
print(transpose)

//実行結果

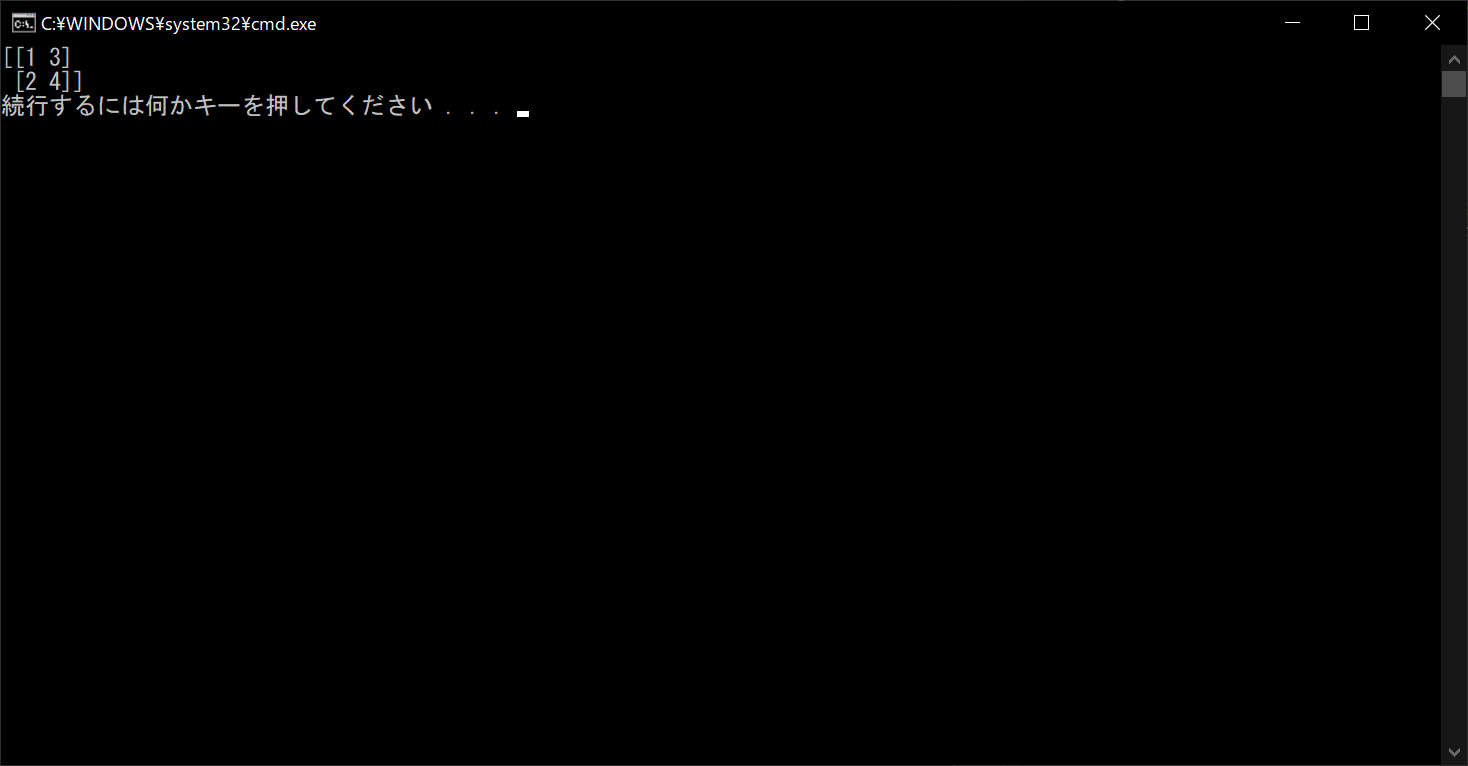
2つの行列の積を求めるときは、「dot関数」を使用します。なぜなら、行列の積は「片方の行ベクトルと列ベクトルの内積」によって求められるからです。「*演算子」を使用すると、単に各要素同士の積が計算されてしまうので注意が必要です。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2つの行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[5, 6], [7, 8]])

# 2つの行列の積を算出する
dotAB = matrixA.dot(matrixB)

# 行列の積を画面上に表示する
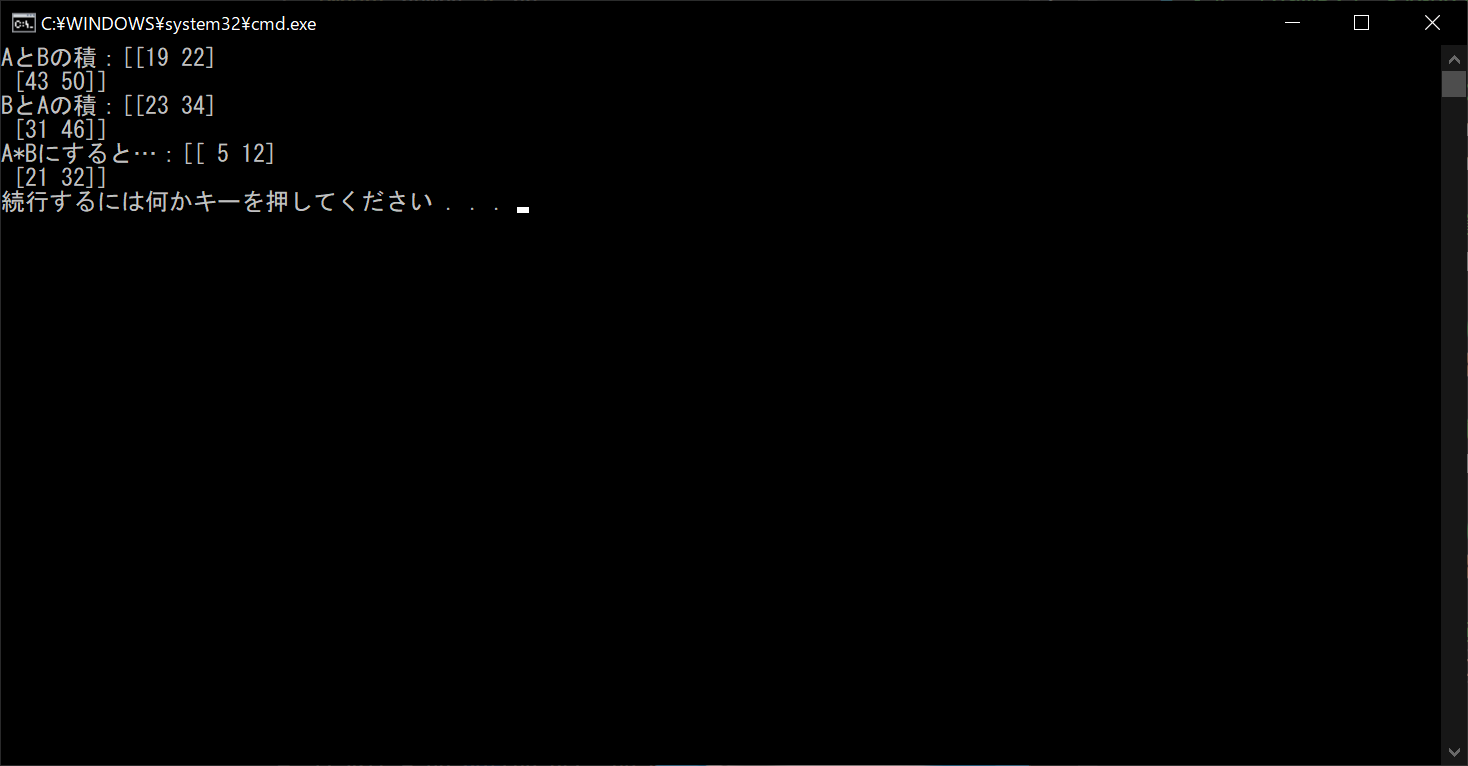
print("AとBの積：{}".format(dotAB))

# 順番を逆にすると解が変わる
dotBA = matrixB.dot(matrixA)

# 行列の積を画面上に表示する
print("BとAの積：{}".format(dotBA))

# 単に「*演算子」を使うと、要素同士の積になるため要注意
print("A*Bにすると…：{}".format(matrixA*matrixB))

//実行結果

PythonのNumPyの基本的な関数と使い方

PythonのNumPyを使いこなすために、まずは以下9つの基本的な使い方を覚えておきましょう。

行列のトータルの要素数を確認する
行列の次元ごとの要素数を確認する
行列の個別の要素にアクセスする
指定した形に行列を変換する
単位行列を取得する
ゼロ行列を取得する
三角行列を取得する
転置行列を取得する
逆行列を取得する

行列のトータルの要素数を確認する

行列のトータルの要素数は「sizeプロパティ」で確認できます。詳細を以下のサンプルコードで確認してみましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])

# 「numpy」で2×4型の行列を生成する
matrixB = numpy.array([[1, 2, 3, 4], [5, 6, 7, 8]])

# 「numpy」で2×3型の行列を生成する
matrixC = numpy.array([[1, 2, 3], [4, 5, 6]])

# 3つの行列の要素数を表示する
print("matrixAのサイズ：{}".format(matrixA.size))
print("matrixBのサイズ：{}".format(matrixB.size))
print("matrixCのサイズ：{}".format(matrixC.size))

//実行結果

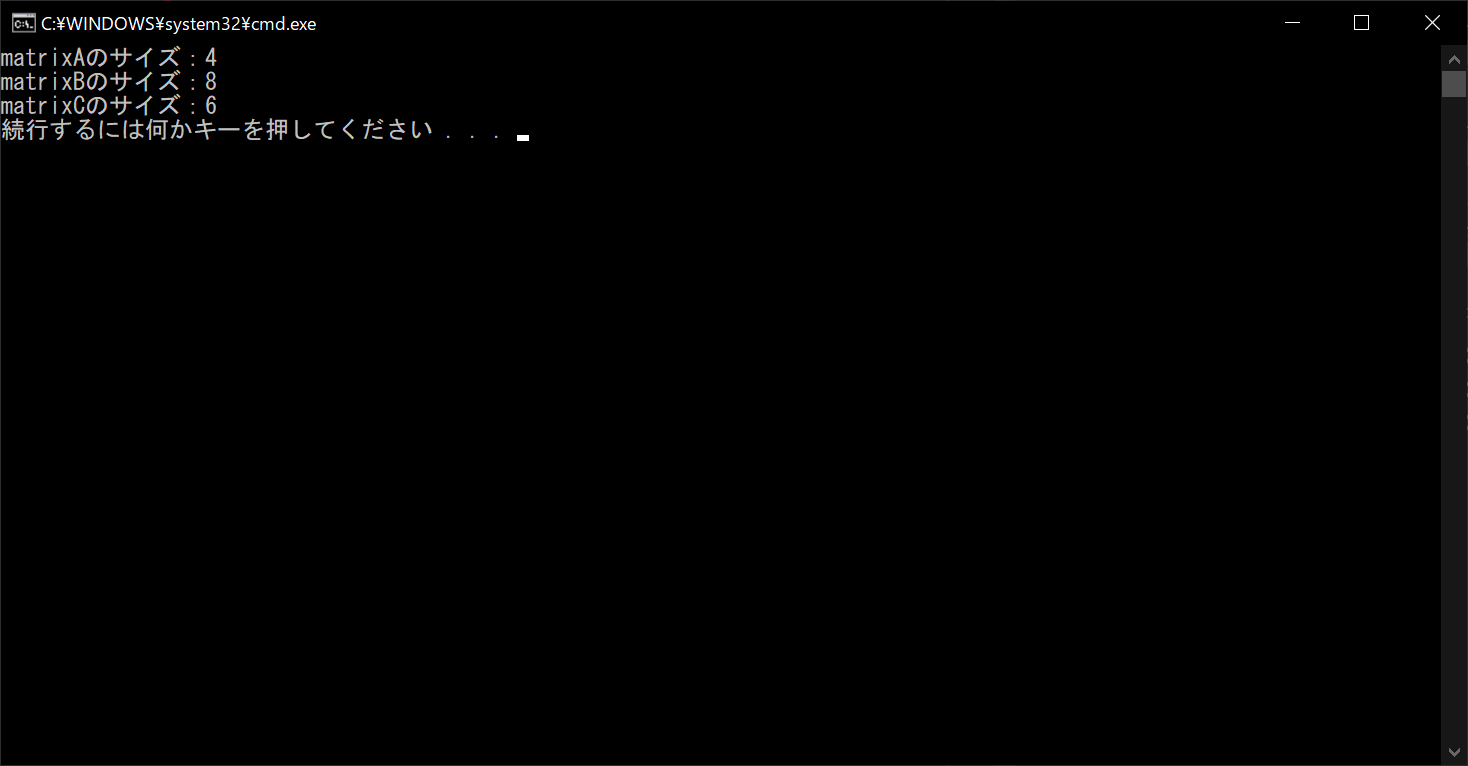
sizeプロパティは単に要素数のトータルを表示するものなので、行列の形状に影響されません。たとえば、2×6型の行列と4×3型の行列のsizeプロパティの値は、いずれも12となります。

行列の次元ごとの要素数を確認する

行列を扱うときに「行と列の要素がそれぞれいくつあるか」調べたいときがあります。そんなときは、以下のサンプルコードのように「shapeプロパティ」を使えば、行列の形状が簡単に分かります。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])

# 「numpy」で2×4型の行列を生成する
matrixB = numpy.array([[1, 2, 3, 4], [5, 6, 7, 8]])

# 「numpy」で2×3型の行列を生成する
matrixC = numpy.array([[1, 2, 3], [4, 5, 6]])

# 3つの行列の形状を表示する
print("matrixAの形状：{}".format(matrixA.shape))
print("matrixBの形状：{}".format(matrixB.shape))
print("matrixCの形状：{}".format(matrixC.shape))

//実行結果

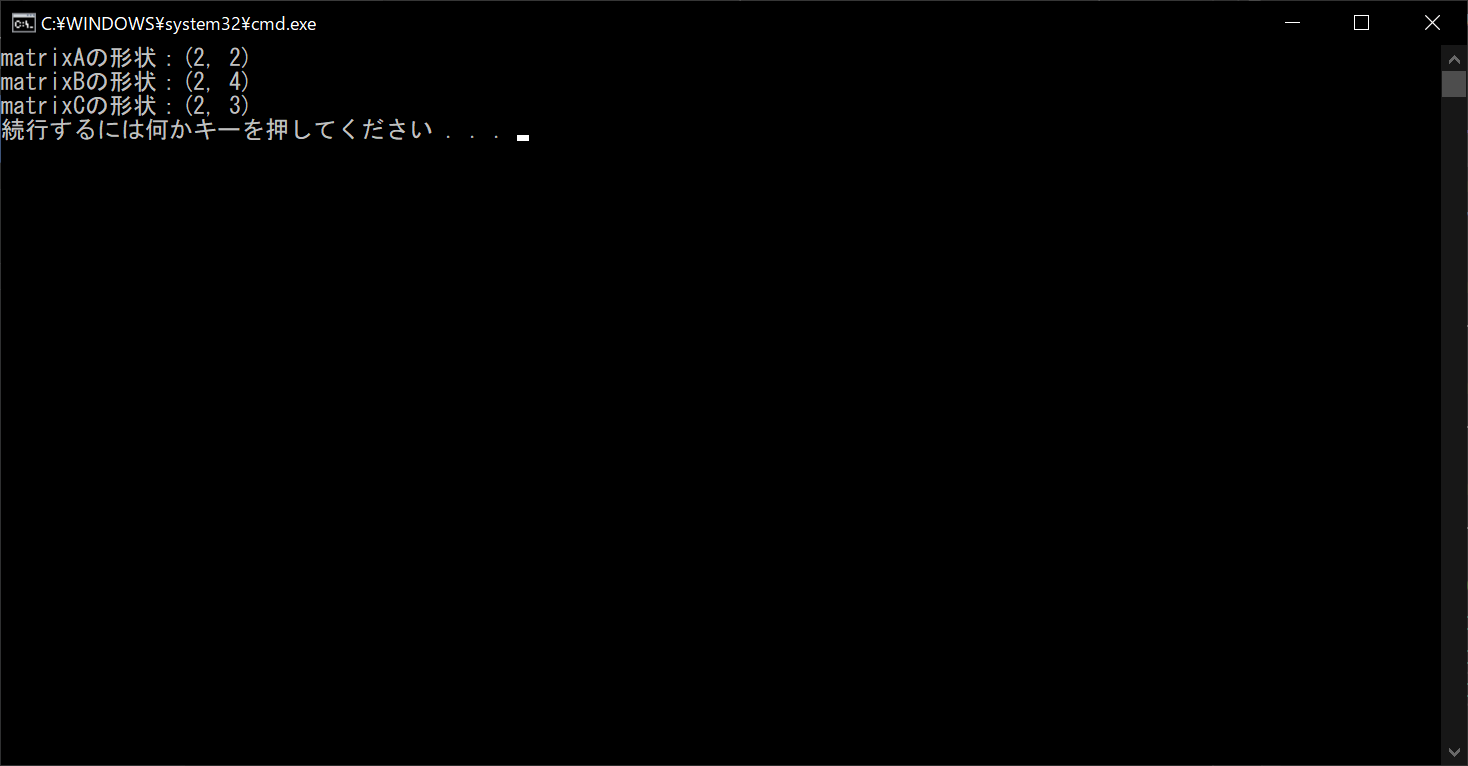
NumPyのshapeプロパティは、行列の形状を「(行数, 列数)」のフォーマットで返します。たとえば(2, 4)は2×4型、(3, 2)は3×2型の行列を意味します。

行列の個別の要素にアクセスする

行列の個別の要素にアクセスしたい場合は、「行列変数名[行番号, 列番号]」の構文を使いましょう。ただし、行番号と列番号は「0」から始まるので、通常の行列で使う番号から「1」を引いたものを指定する必要があります。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で3×3型の行列を生成する
matrix = numpy.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 行列の中身を表示する
print(matrix)

# (1, 1)の要素にアクセスする
print("(1, 1)の要素：{}".format(matrix[0, 0]))

# (3, 3)の要素にアクセスする
print("(3, 3)の要素：{}".format(matrix[2, 2]))

# (2, 1)の要素にアクセスする
print("(2, 1)の要素：{}".format(matrix[1, 0]))

//実行結果

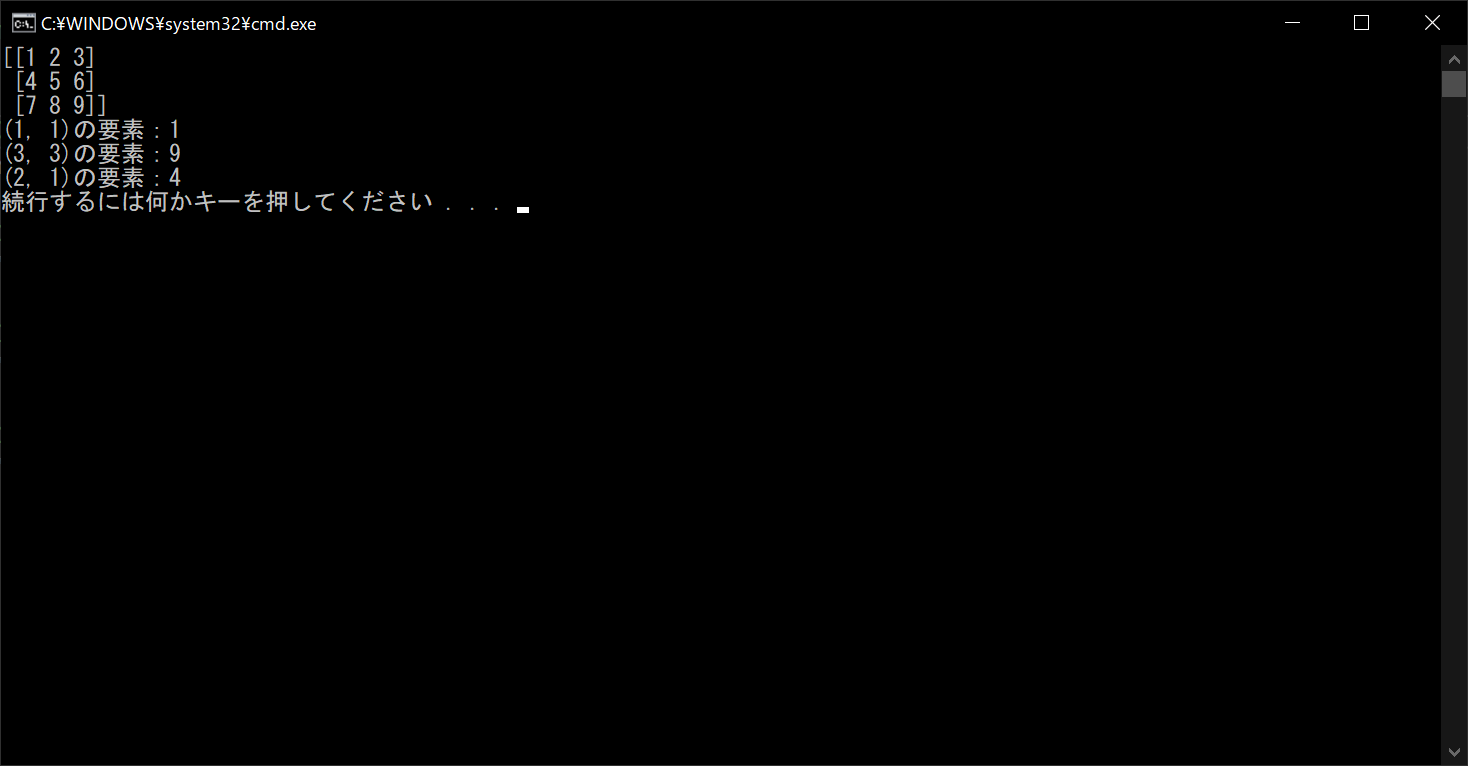
「[行数, 列数]」の形式で指定すると、該当する行列の要素にアクセスできます。ただし、指定する番号はリストのインデックスなので注意が必要です。たとえば、行列の(1, 2)にアクセスしたいときは、[0, 1」と指定する必要があります。また、リストの範囲外のインデックスを指定するとエラーが出ます。

指定した形に行列を変換する

行列の形状を変更したいときは、「reshape関数」の引数で形状を指定すると、行列を簡単に変換できます。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])

# 「numpy」で4×4型の行列を生成する
matrixB = numpy.array([[1, 2, 3, 4], [5, 6, 7, 8]])

# 「numpy」で2×3型の行列を生成する
matrixC = numpy.array([[1, 2, 3], [4, 5, 6]])

# 2×2型の行列を1×4行列に変換する
print("matrixAを1×4行列に変換：{}".format(matrixA.reshape(1, 4)))

# 4×2型の行列を2×4行列に変換する
print("matrixBを2×4行列に変換：{}".format(matrixB.reshape(2, 4)))

# 2×3型の行列を3×2行列に変換する
print("matrixCを3×2行列に変換：{}".format(matrixC.reshape(3, 2)))

//実行結果

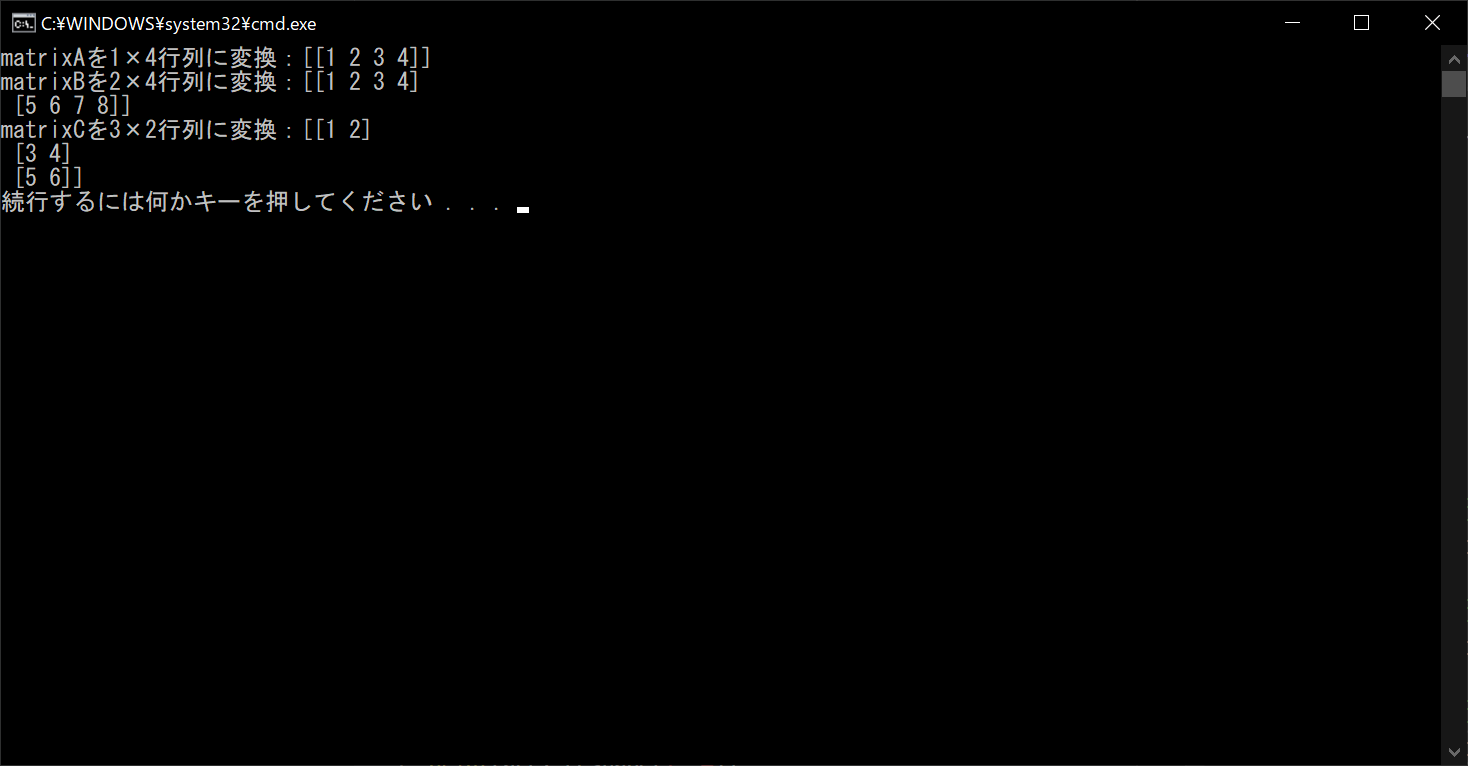
なお、トータルの要素数が異なる形状を指定すると、エラーが出るので注意しましょう。たとえば、2×3型の行列は要素数が6なので、要素数がそれより大きい3×3行列や、小さい2×2行列には変換できません。

単位行列を取得する

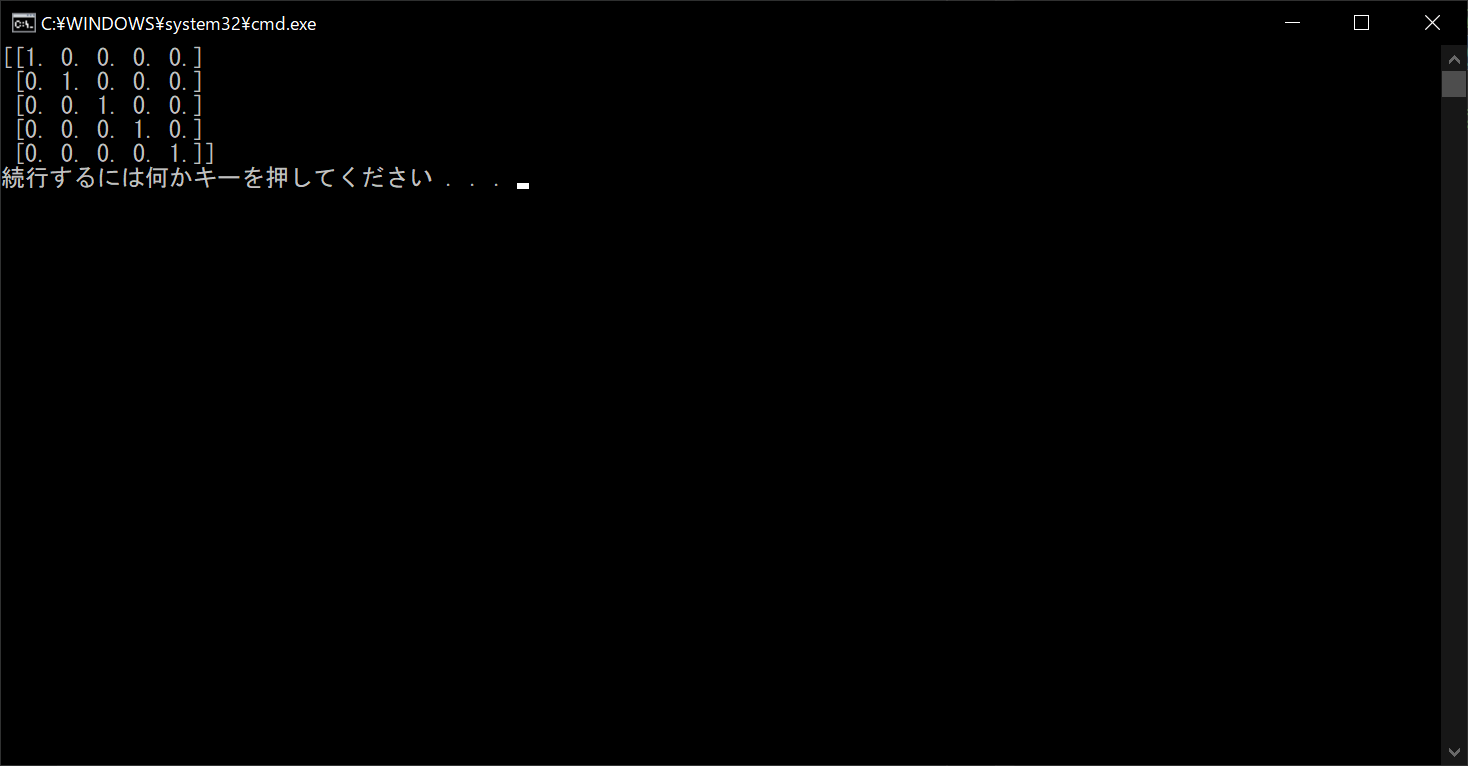
NumPyで単位行列を取得したい場合は、「identity関数」の引数に行列の数を指定すればOKです。なお単位行列とは、行列の「対角の成分」がすべて「1」で、それ以外が「0」の行列を指します。
対角の成分は（1, 1）や（2, 2）などのように、左上隅から右下隅に向かって並ぶ成分のことです。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で5×5型の単位行列を生成する
matrix = numpy.identity(5)

# 5×5型の単位行列を表示する
print(matrix)

//実行結果

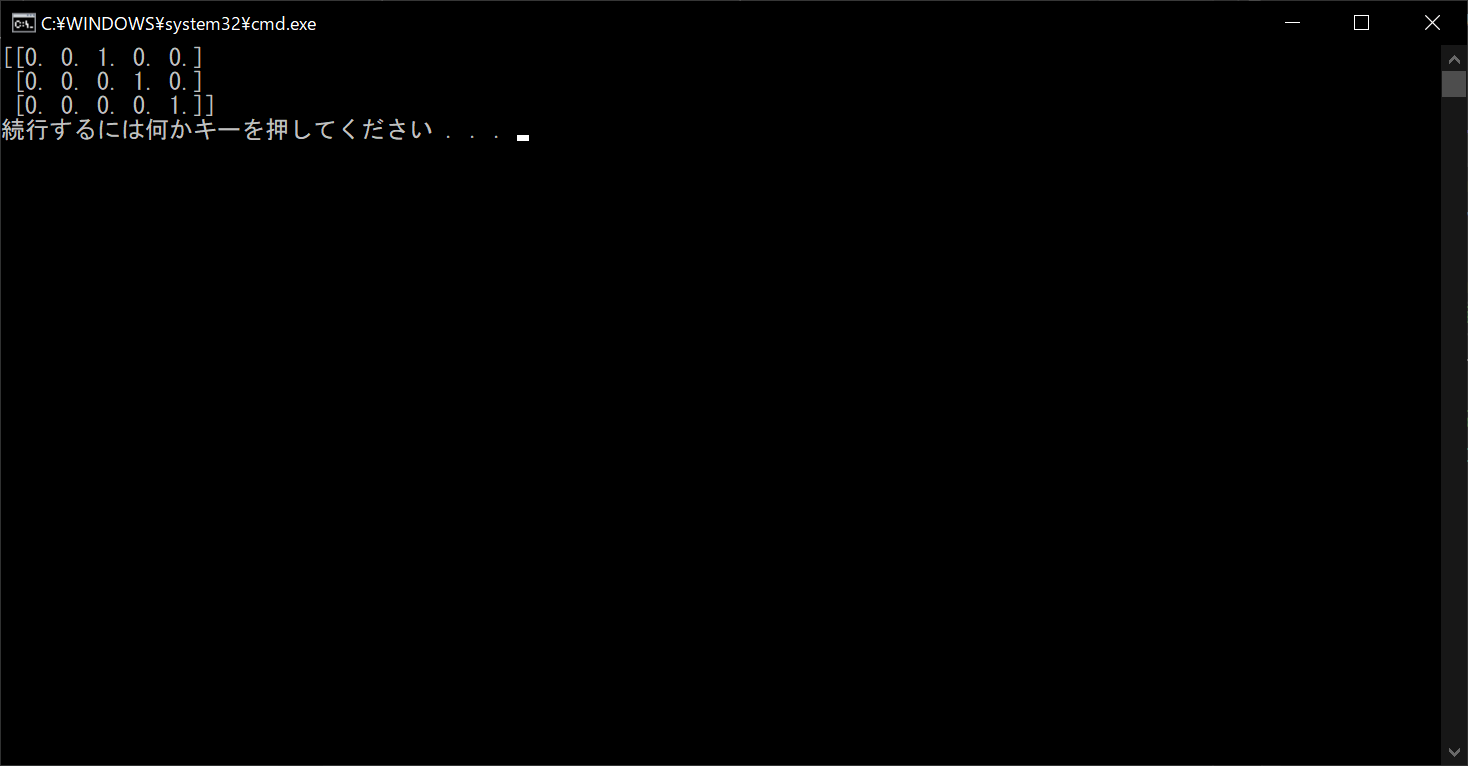
なお行と列の数を変えたい場合は、以下のサンプルコードのように「eye関数」の引数で、行数・列数・対角線のスタート位置を指定しましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で3×5型の単位行列を生成する
# 対角線は3番目（インデックスでは2番目）から始まるように設定する
matrix = numpy.eye(3, 5, 2)

# 3×5型の単位行列を表示する
print(matrix)

//実行結果

ゼロ行列を取得する

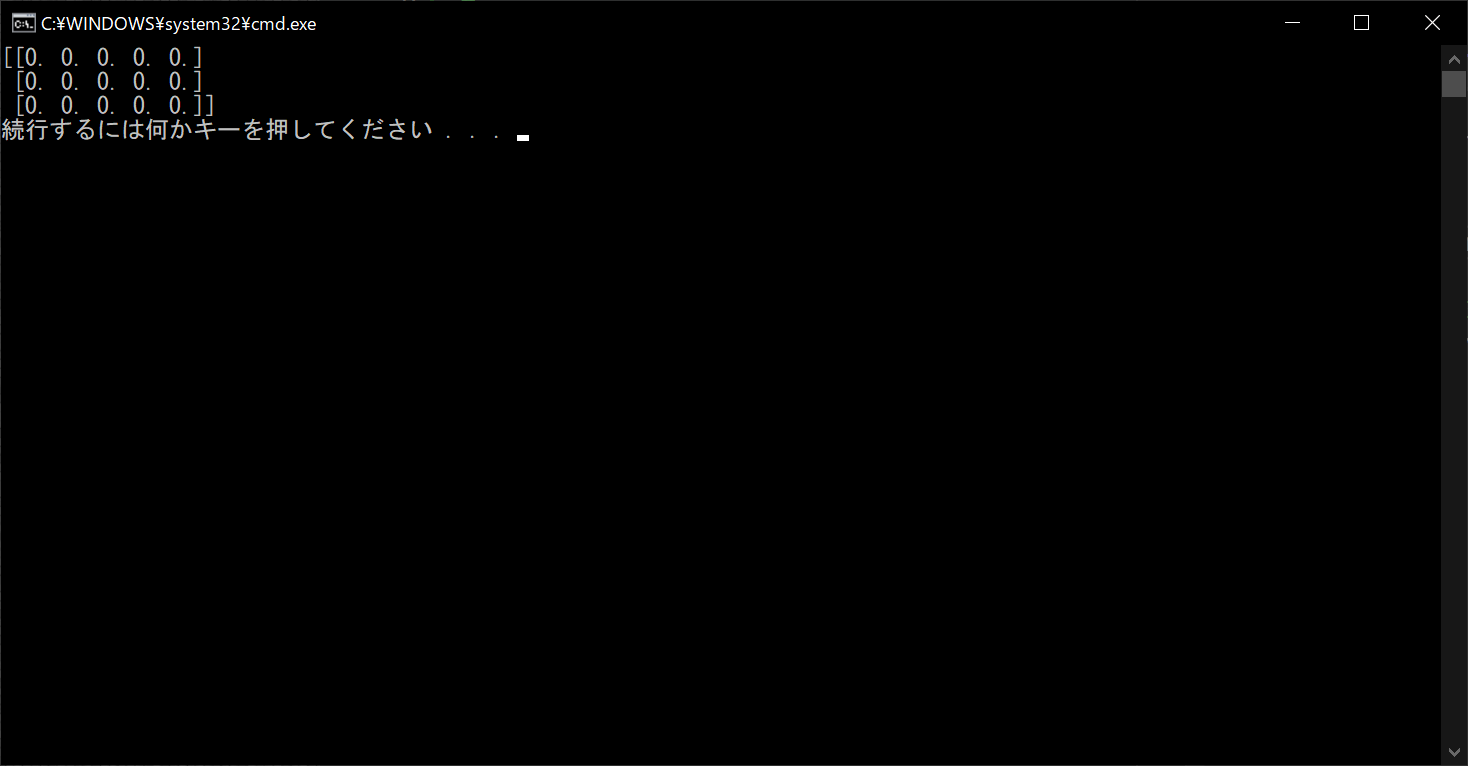
すべての要素が「0」で構成されているゼロ行列は、「zeros関数」の引数にタプル形式で行数と列数を指定しましょう。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で3×5型のゼロ行列を生成する
matrix = numpy.zeros((3, 5))

# 3×5型のゼロ行列を表示する
print(matrix)

//実行結果

三角行列を取得する

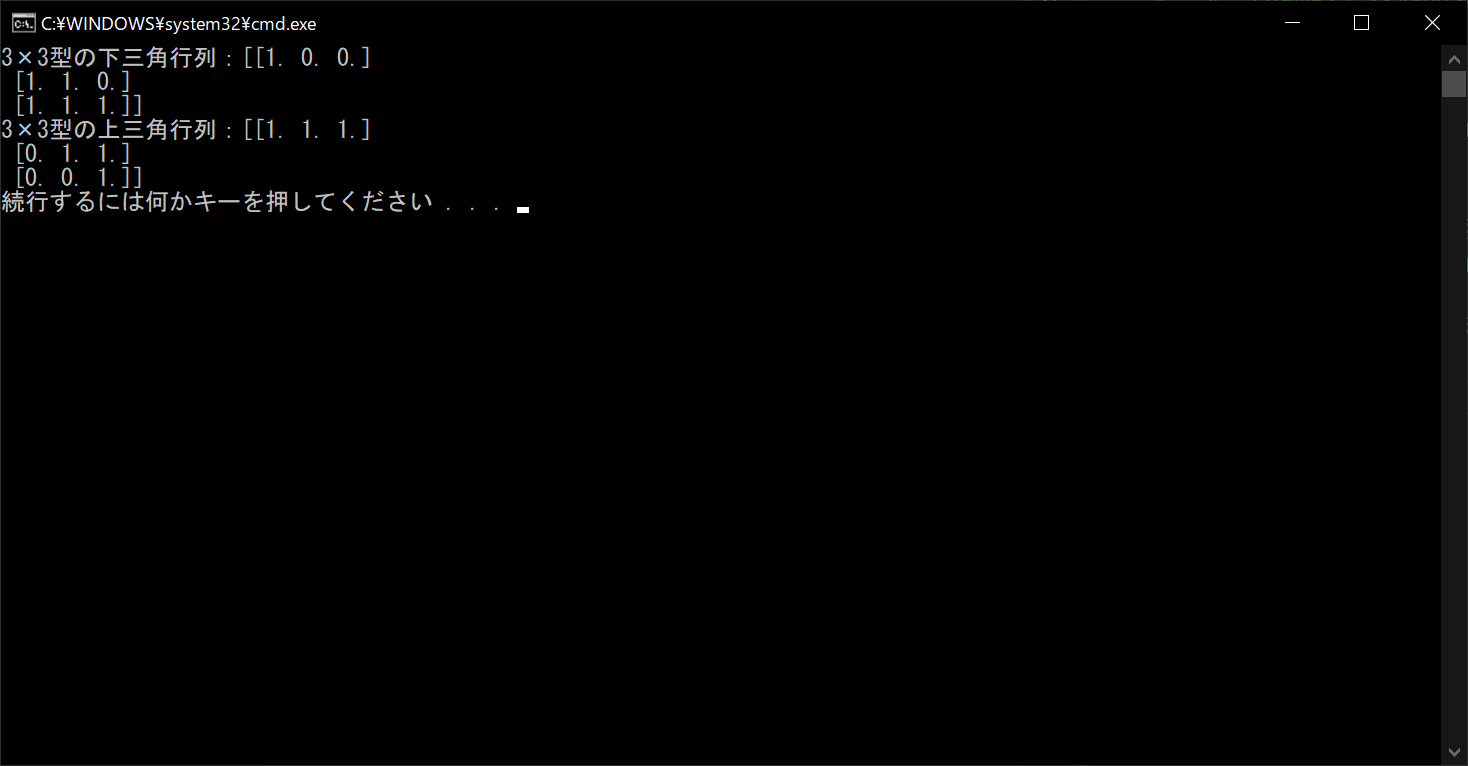
対角成分より上側の成分が0である「下三角行列」は、「tri関数」に行列の数を指定すれば簡単に作成できます。ただし、対角成分より下側の成分が0である「上三角行列」を生成する関数はないので、下三角行列を「transpose関数」で転置させる必要があります。詳細を以下のサンプルコードで確認しましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で3×3型の下三角行列を生成する
matrixA = numpy.tri(3)

# 「numpy」で3×3型の上三角行列を生成する
# 上三角行列を生成する関数はないので、transpose関数で転置行列にする
matrixB = numpy.tri(3).transpose()

# それぞれの三角行列を表示する
print("3×3型の下三角行列：{}".format(matrixA))
print("3×3型の上三角行列：{}".format(matrixB))

//実行結果

転置行列を取得する

前述したように、転置行列は「Tプロパティ」で取得できますが、「transpose関数」でも同じように転置行列を算出できます。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])

# 「numpy」で4×4型の行列を生成する
matrixB = numpy.array([[1, 2, 3, 4], [5, 6, 7, 8]])

# 「numpy」で2×3型の行列を生成する
matrixC = numpy.array([[1, 2, 3], [4, 5, 6]])

# matrixAの転置行列を表示する
print("matrixAの転置行列：{}".format(matrixA.transpose()))

# matrixBの転置行列を表示する
print("matrixBの転置行列：{}".format(matrixB.transpose()))

# matrixCの転置行列を表示する
print("matrixCの転置行列：{}".format(matrixC.transpose()))

//実行結果

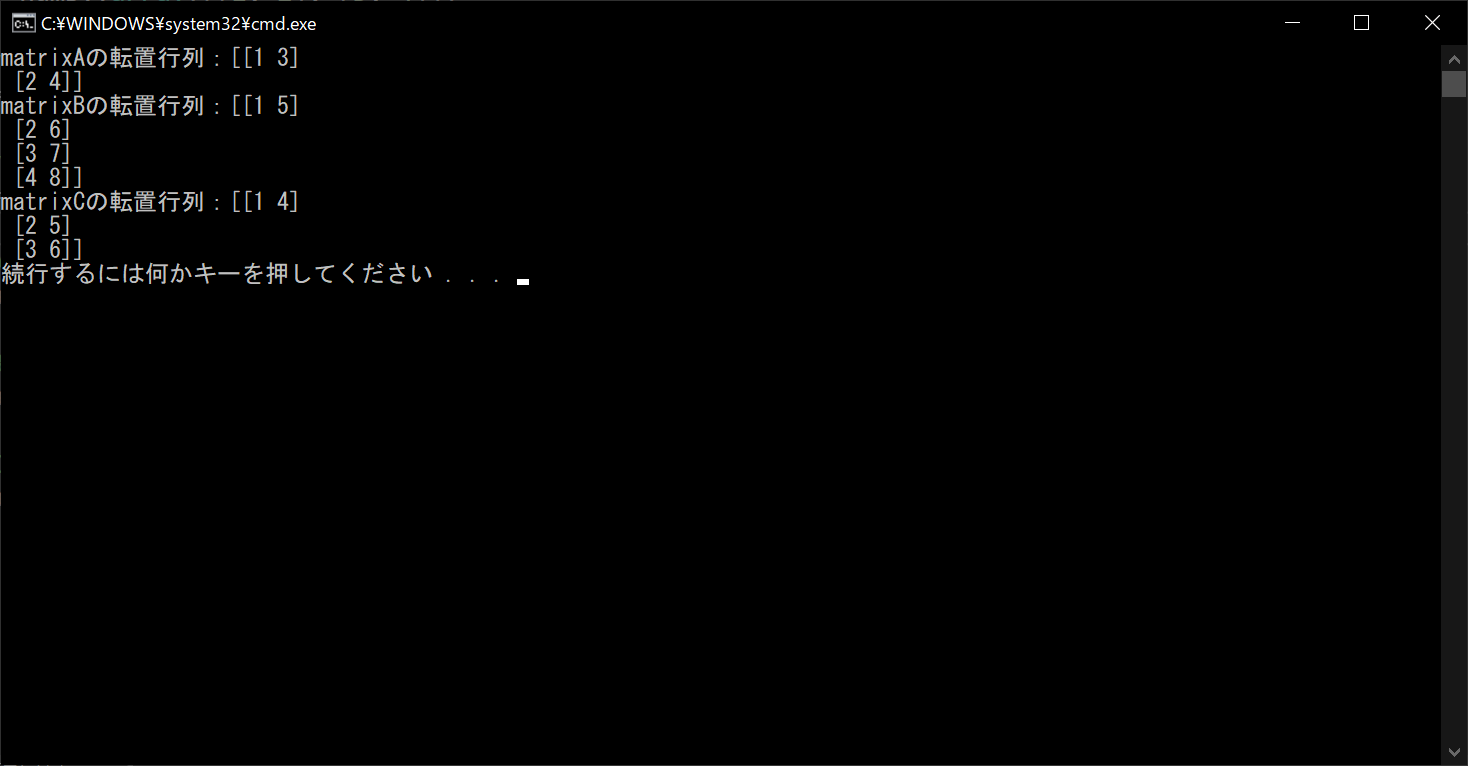
逆行列を取得する

ある行列Aに対して、「AY・YA = E（単位行列）」となる行列Yを、行列Aの「逆行列」と呼びます。逆行列を算出したいときは、「numpy.linalg.inv関数」の引数に、元の行列を渡しましょう。なお逆行列は「正方行列」でなければ定義できないので、変換元の行列は「行と列の要素数が同じ」でないといけません。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を生成する
matrix = numpy.array([[2, -1], [-3 ,4]])

# 逆行列を生成する
inverse = numpy.linalg.inv(matrix)

# 逆行列を表示する
print("matrixの逆行列：{}".format(inverse))

# 「matrix・inverse」の値が単位行列になるかチェックする
print("matrix・inverse：{}".format(matrix.dot(inverse)))

//実行結果

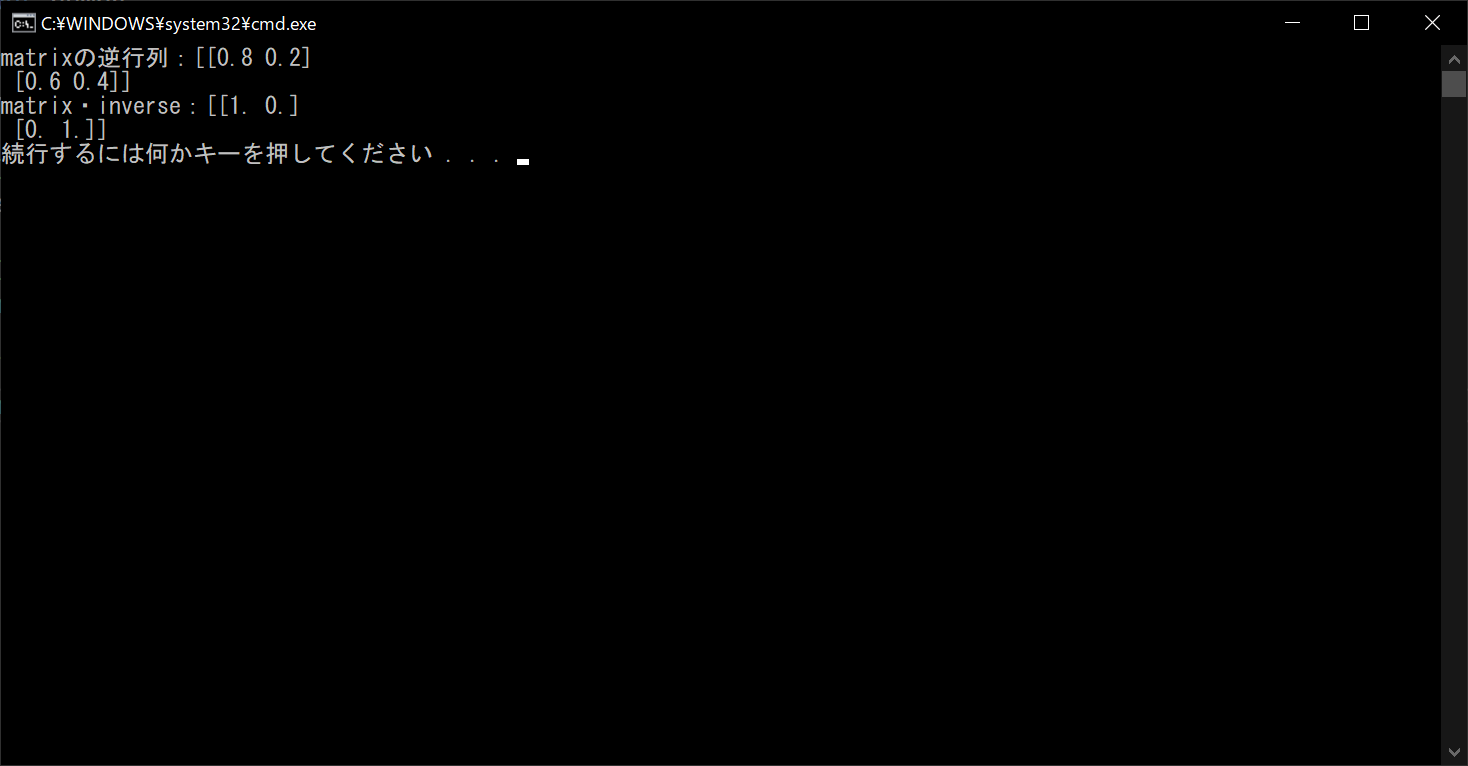
ただし行列要素の値によっては、正方行列であっても逆行列を算出できないので注意が必要です。たとえば行列式がゼロになる場合は、特異行列なので逆行列が存在せず、画面上にエラーが表示されます。ただし「numpy.linalg.pinv関数」を使えば、正確ではありませんが「疑似逆行列」を取得できます。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を生成する
matrix = numpy.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 疑似逆行列を生成する
inverse = numpy.linalg.pinv(matrix)

# 疑似逆行列を表示する
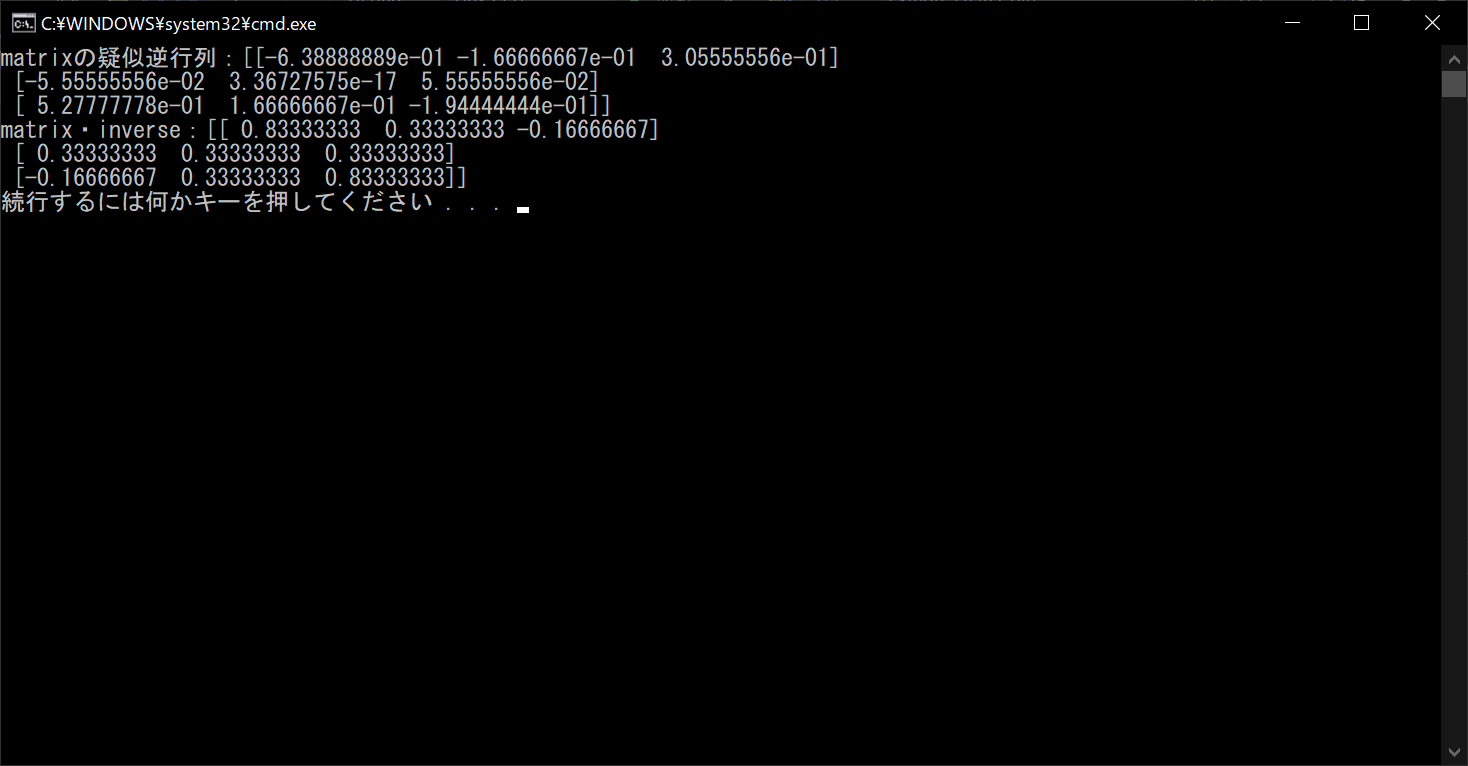
print("matrixの疑似逆行列：{}".format(inverse))

# 「matrix・inverse」の値が単位行列になるかチェックする
print("matrix・inverse：{}".format(matrix.dot(inverse)))

//実行結果

NumPyでさまざまな行列演算を試してみよう！

これまでに紹介してきた知識を踏まえて、実際に行列の「四則演算」を行ってみましょう。ただし、行列の乗算（掛け算）に関しては、スカラー（通常の数値）の感覚とはまったく異なるので注意が必要です。

行列の足し算
行列の引き算
行列の掛け算
行列の割り算

それぞれ解説します。

行列の足し算

行列同士の足し算は、通常のスカラーの計算と同じで、各要素同士の値を単純に足し合わせるだけです。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を2つ生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[5, 6], [7, 8]])

# 「matrixA + matrixB」を算出する
result = matrixA + matrixB

# 演算結果を表示する
print("matrixA + matrixB：{}".format(result))

//実行結果

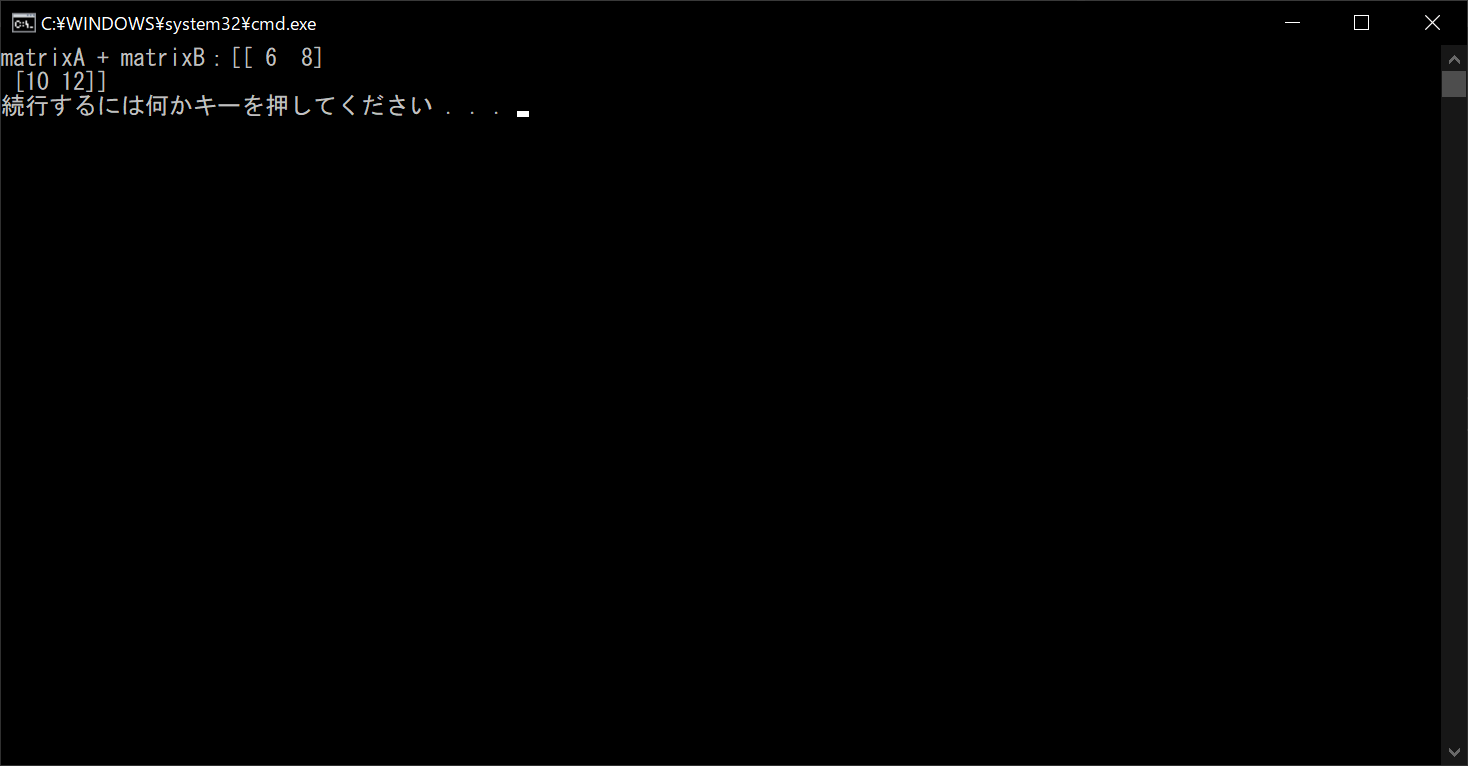
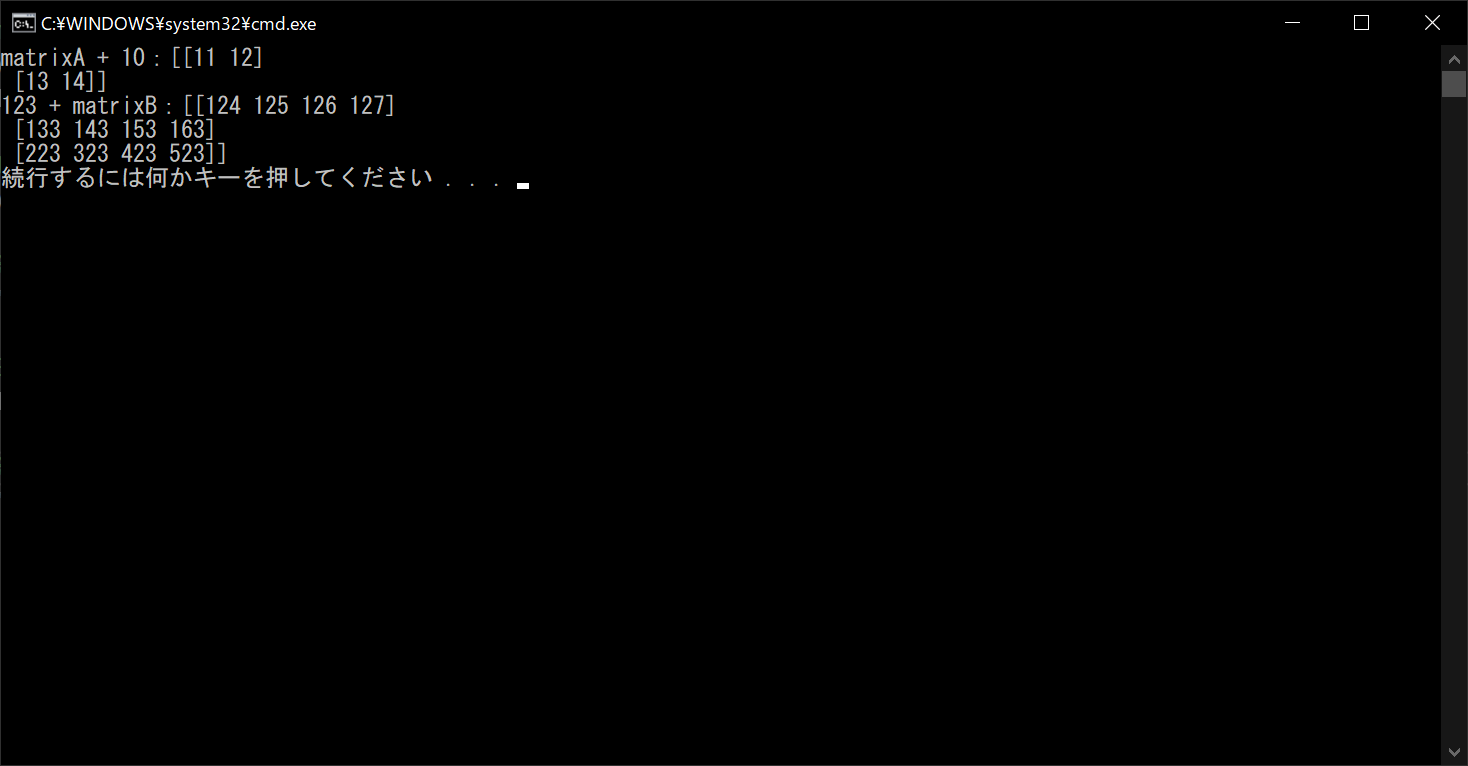
ちなみに行列同士だけではなく、行列とスカラーの足し算もできます。その場合は、行列のすべての要素にスカラーの値を足すことになります。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2つの行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[1, 2, 3, 4], [10, 20, 30, 40], [100, 200, 300, 400]])

# 「matrixA + 10」を算出する
resultA = matrixA + 10

# 演算結果を表示する
print("matrixA + 10：{}".format(resultA))

# 「123 + matrixB」を算出する
resultB = 123 + matrixB

# 演算結果を表示する
print("123 + matrixB：{}".format(resultB))

//実行結果

行列の引き算

行列同士の引き算も、足し算と同じで各要素同士の値を単純に引くだけです。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を2つ生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[5, 6], [7, 8]])

# 「matrixA - matrixB」を算出する
result = matrixA - matrixB

# 演算結果を表示する
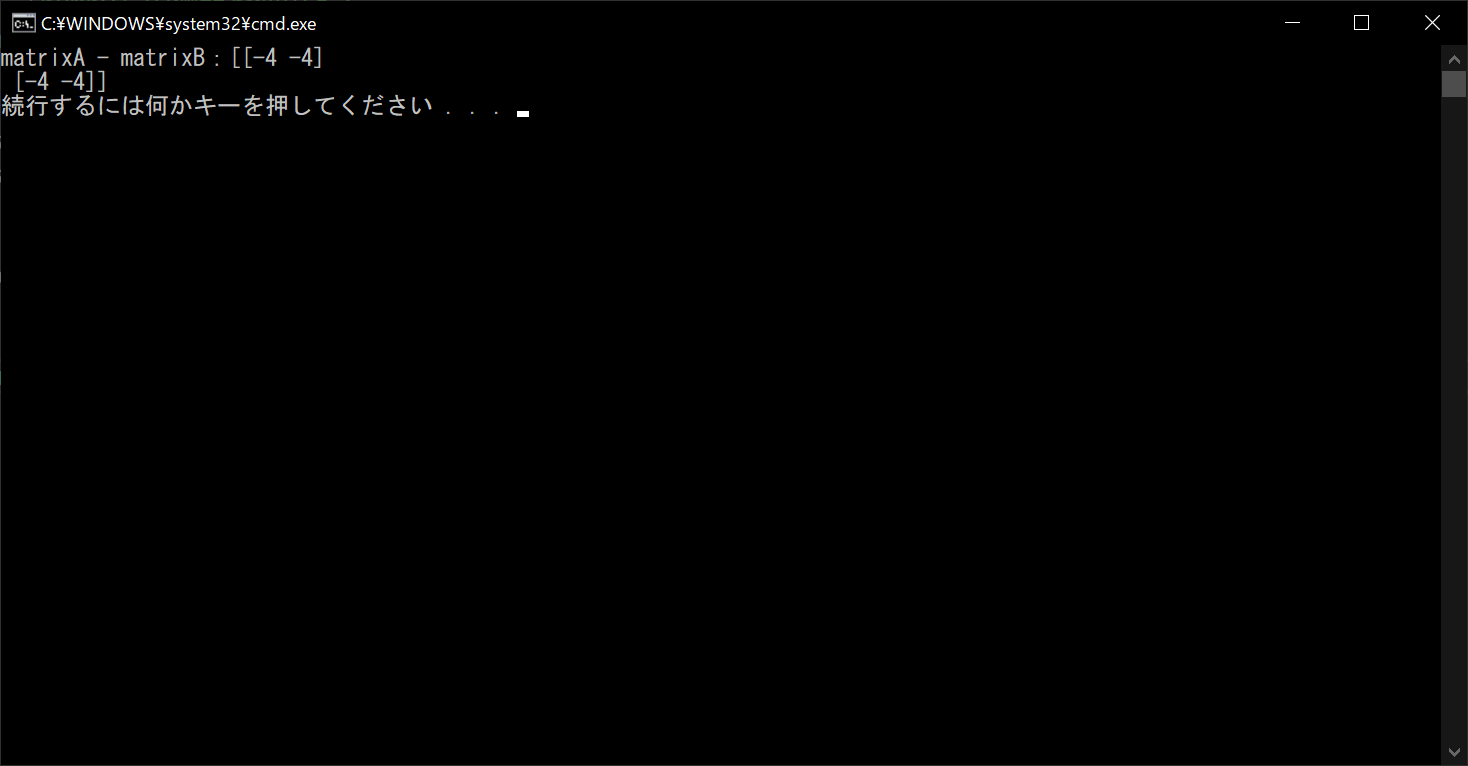
print("matrixA - matrixB：{}".format(result))

//実行結果

足し算と同じように、行列とスカラーの引き算もできます。行列のすべての要素からスカラーの値を引けるので、大量のデータを処理するときに便利です。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2つの行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[1, 2, 3, 4], [10, 20, 30, 40], [100, 200, 300, 400]])

# 「matrixA - 10」を算出する
resultA = matrixA - 10

# 演算結果を表示する
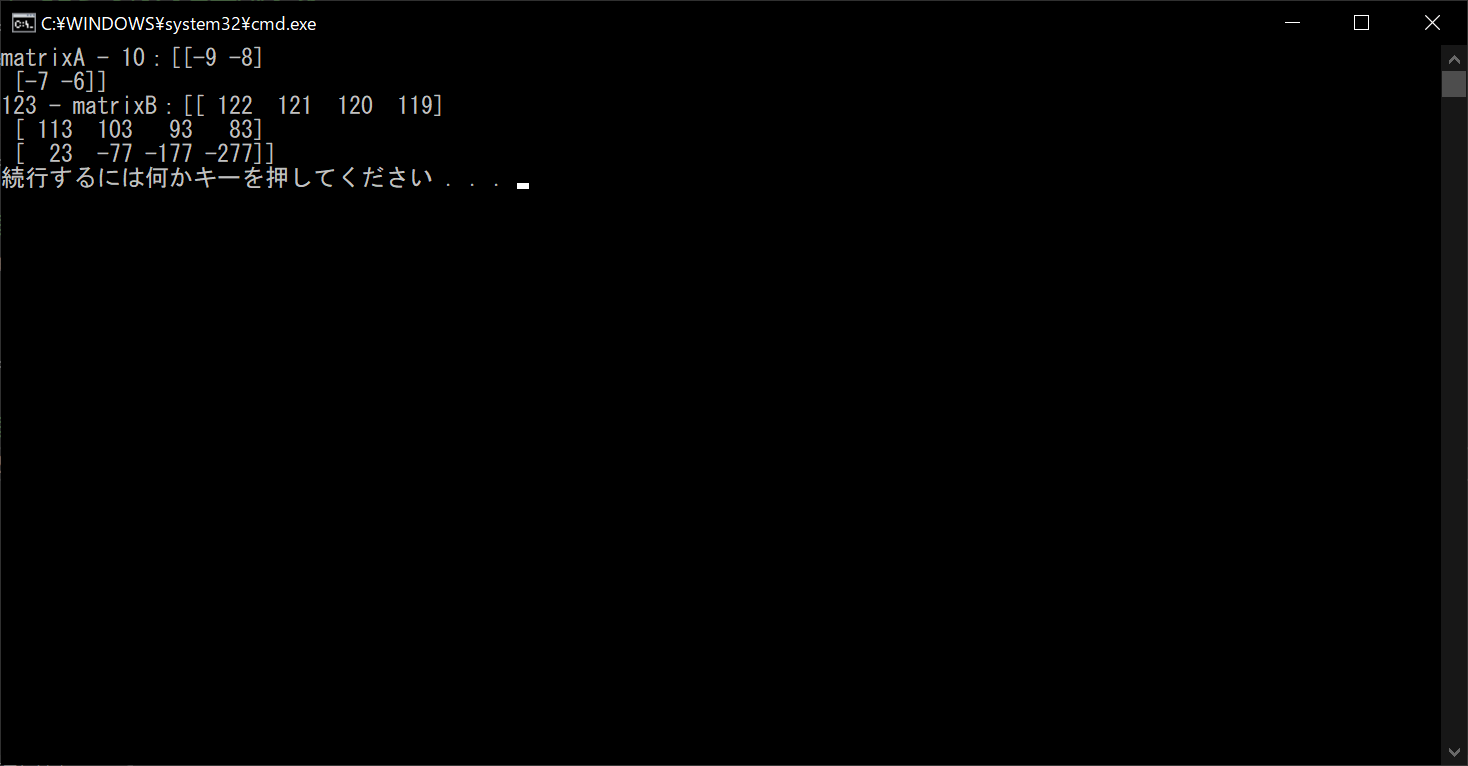
print("matrixA - 10：{}".format(resultA))

# 「123 - matrixB」を算出する
resultB = 123 - matrixB

# 演算結果を表示する
print("123 - matrixB：{}".format(resultB))

//実行結果

行列の掛け算

NumPyによる行列演算で特に注意が必要なのが掛け算です。行列の掛け算には、足し算や引き算のように単純に各要素同士を掛け合わせるものと、行列の内積を求めるものの2種類があります。単純な掛け算の場合は「*演算子」、内積を求める場合は「dot関数」を使用します。詳細を以下のサンプルコードで確認しましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を2つ生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[5, 6], [7, 8]])

# 「matrixA * matrixB」を算出する
resultA = matrixA * matrixB

# 演算結果を表示する
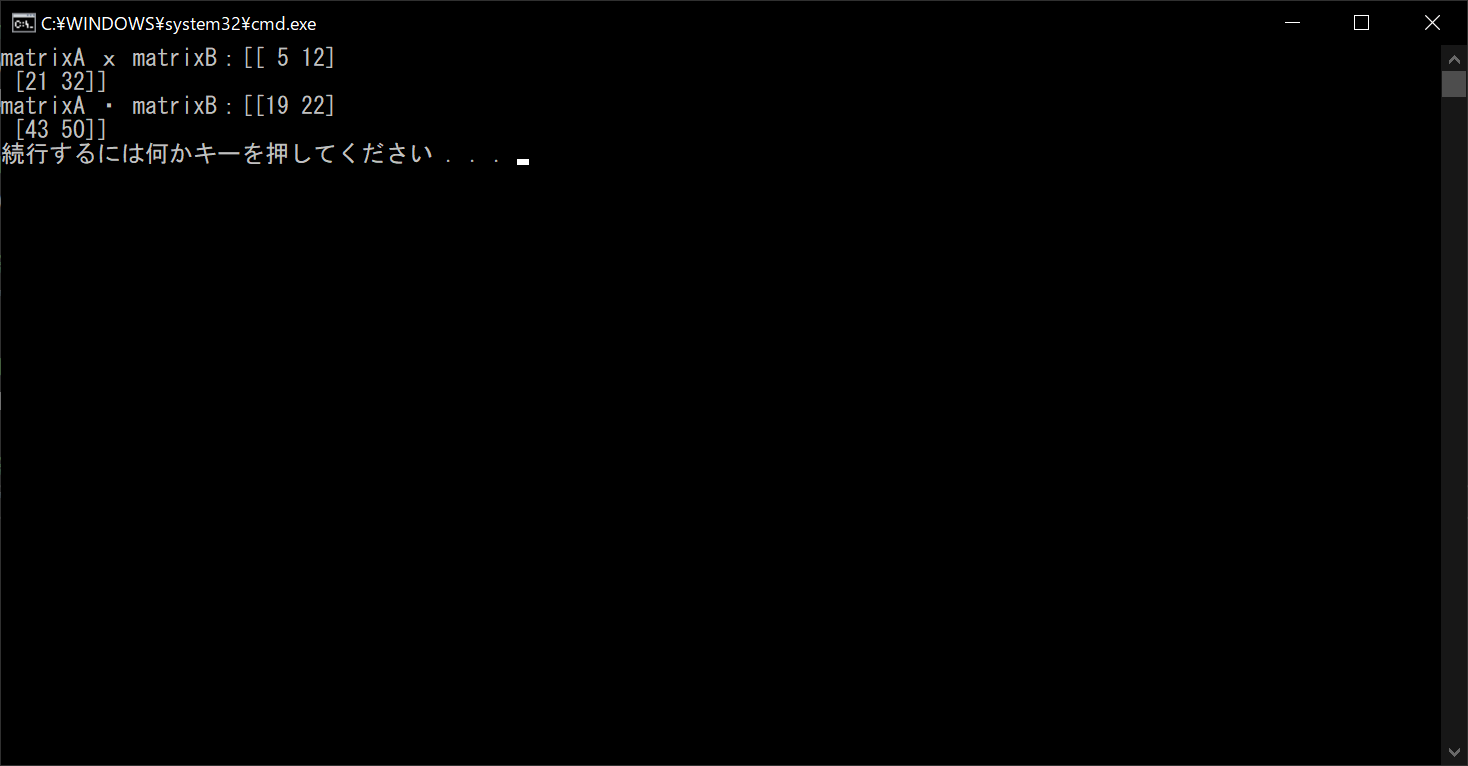
print("matrixA ｘ matrixB：{}".format(resultA))

# 「matrixA・matrixB」を算出する
resultB = matrixA.dot(matrixB)

# 演算結果を表示する
print("matrixA ・ matrixB：{}".format(resultB))

//実行結果

なお、行列とスカラーの積も算出可能です。単に行列とスカラーを掛け合わせるだけで、行列のすべての要素を、スカラー倍できます。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2つの行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[1, 2, 3, 4], [10, 20, 30, 40], [100, 200, 300, 400]])

# 「matrixA * 2」を算出する
resultA = matrixA * 2

# 演算結果を表示する
print("matrixA ｘ 2：{}".format(resultA))

# 「matrixA * 0.5」を算出する
resultB = matrixB * 0.5

# 演算結果を表示する
print("matrixB ｘ 0.5：{}".format(resultB))

//実行結果

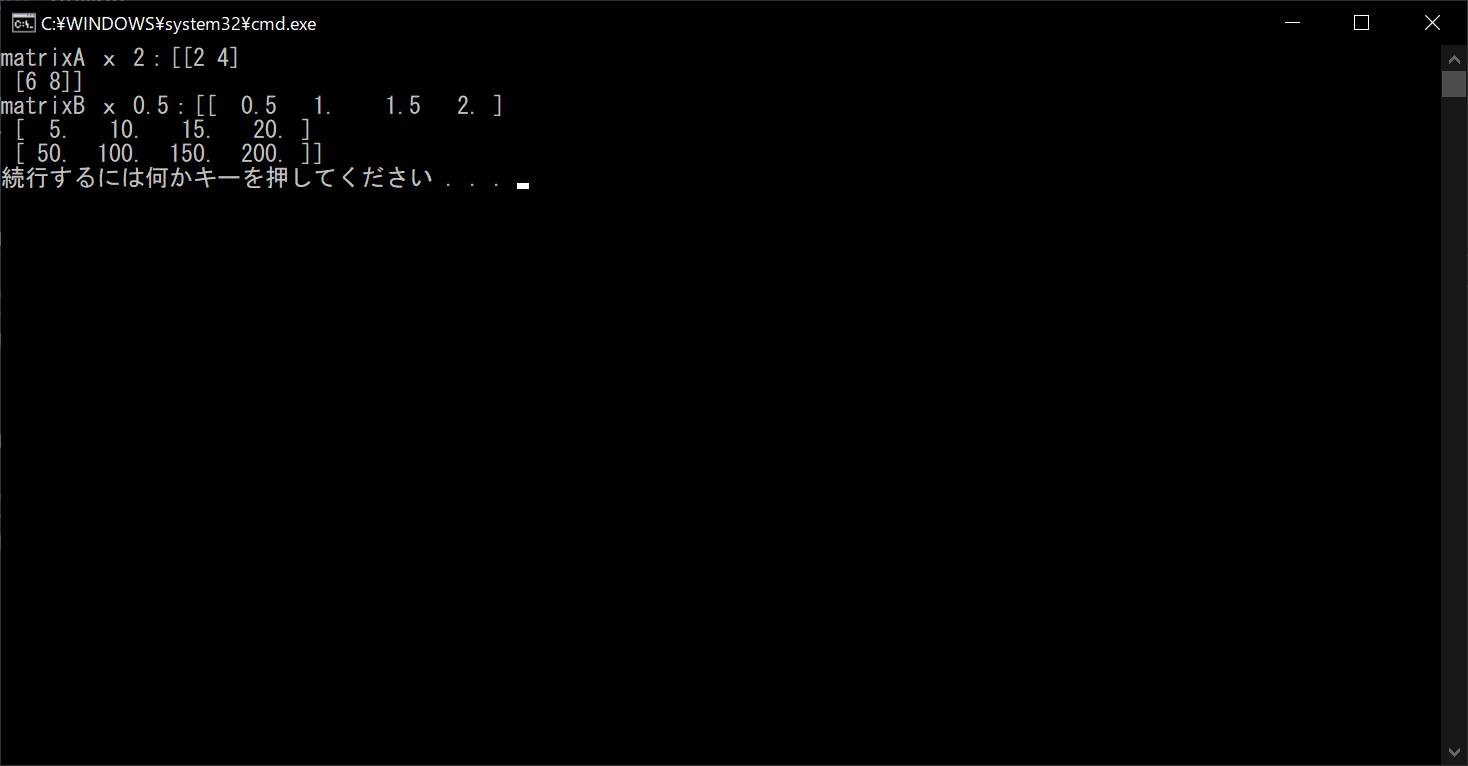
行列とスカラーの乗算は、後述する「画像処理」でよく出てくる処理なので、覚えておきましょう。

行列の割り算

行列の割り算は、足し算と引き算と同じく、単純に各要素同士を割ったものになります。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2×2型の行列を2つ生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[5, 6], [7, 8]])

# 「matrixA / matrixB」を算出する
result = matrixA / matrixB

# 演算結果を表示する
print("matrixA / matrixB：{}".format(result))

//実行結果

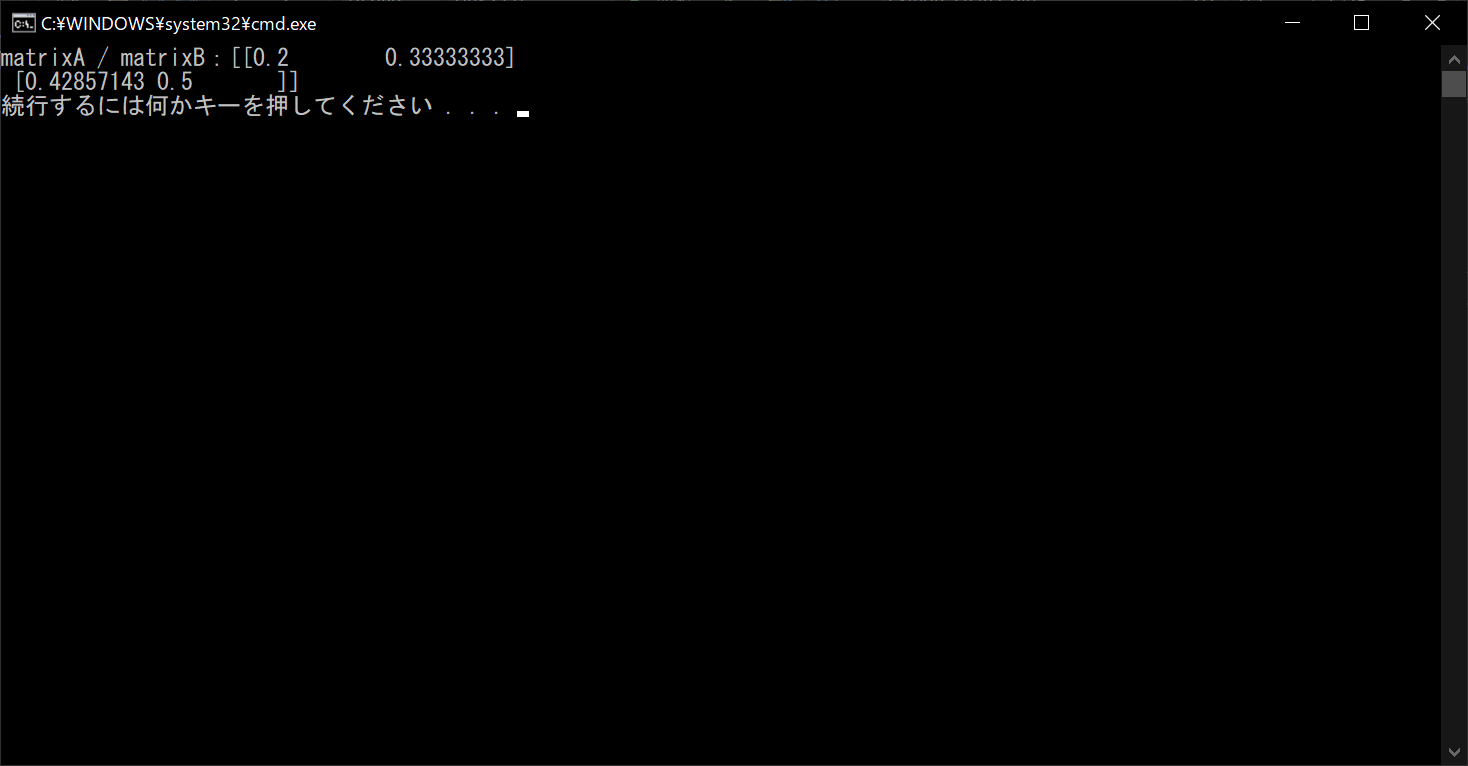
なお掛け算と同様に、行列とスカラーの除算もできます。単に行列をスカラーで割るだけで、行列のすべての要素をスカラーの値で割ることが可能です。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「numpy」で2つの行列を生成する
matrixA = numpy.array([[1, 2], [3, 4]])
matrixB = numpy.array([[1, 2, 3, 4], [10, 20, 30, 40], [100, 200, 300, 400]])

# 「matrixA / 2」を算出する
resultA = matrixA / 2

# 演算結果を表示する
print("matrixA / 2：{}".format(resultA))

# 「matrixA / 0.5」を算出する
resultB = matrixB / 0.5

# 演算結果を表示する
print("matrixB / 0.5：{}".format(resultB))

//実行結果

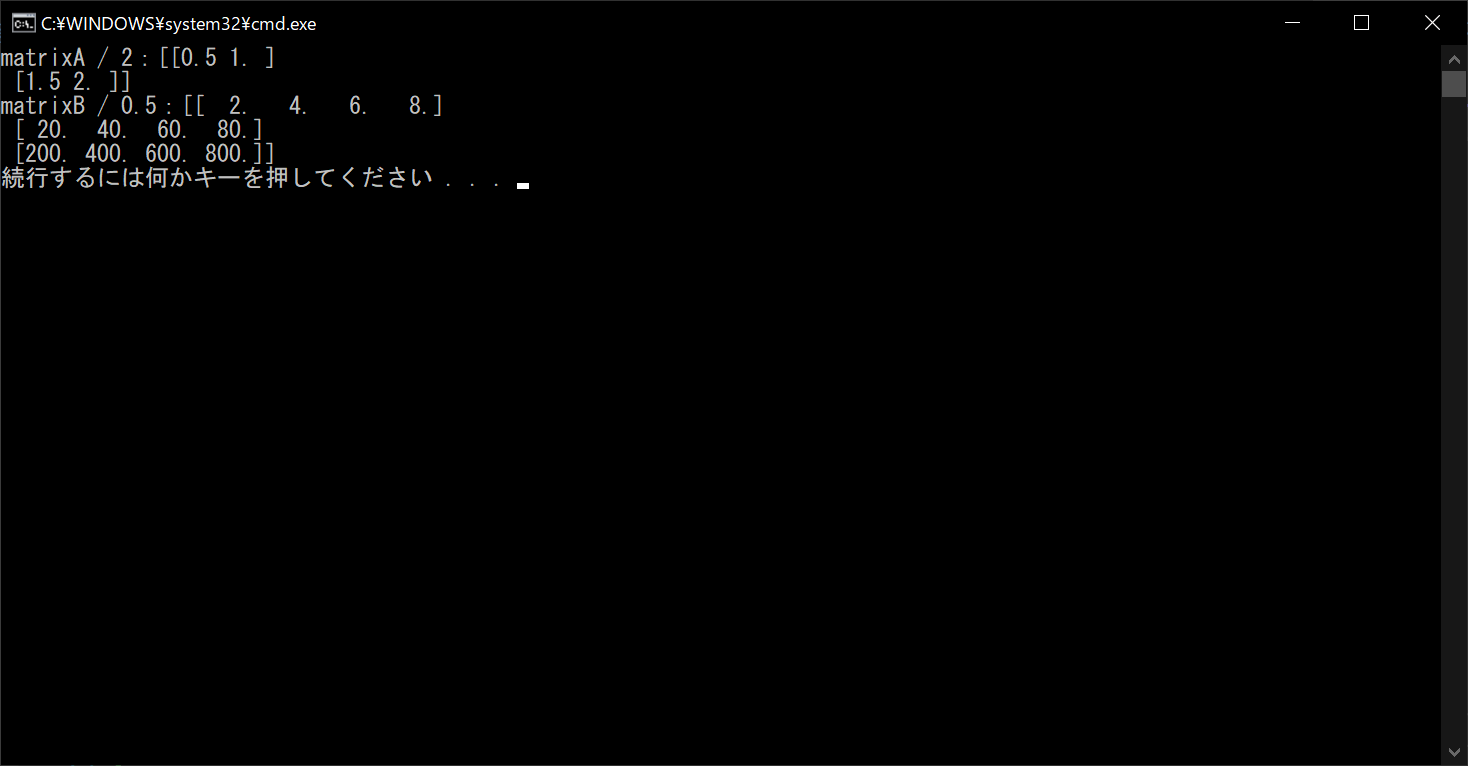
行列とスカラーの除算も、乗算と同様に画像処理でよく活用するので、ここで覚えておきましょう。

【応用編】NumPyで画像データも扱える！

NumPyライブラリの大きな魅力のひとつが、「画像処理」が簡単にできることです。通常、画像処理には専用のツールが必要ですが、NumPyを使えばPythonスクリプトで簡単にできます。

ただしNumPyで画像データを扱うためには、「Pillow（PIL）」というライブラリを利用する必要があります。しかし、Visual StudioにはデフォルトでPillowがインストールされていないため、以下の手順でまずPillowをインストールしましょう。

Pillow（PIL）をVisual Studioにインストールする方法

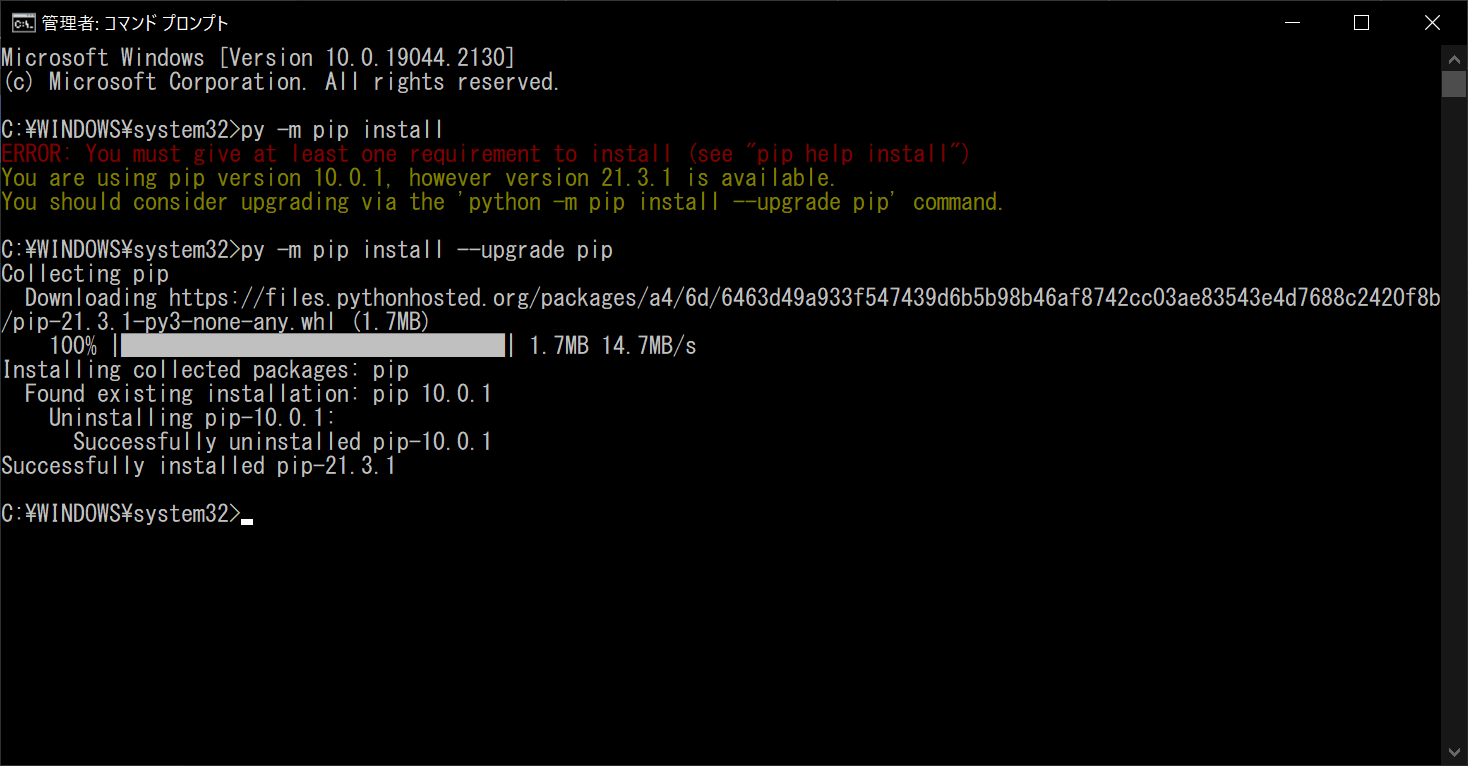
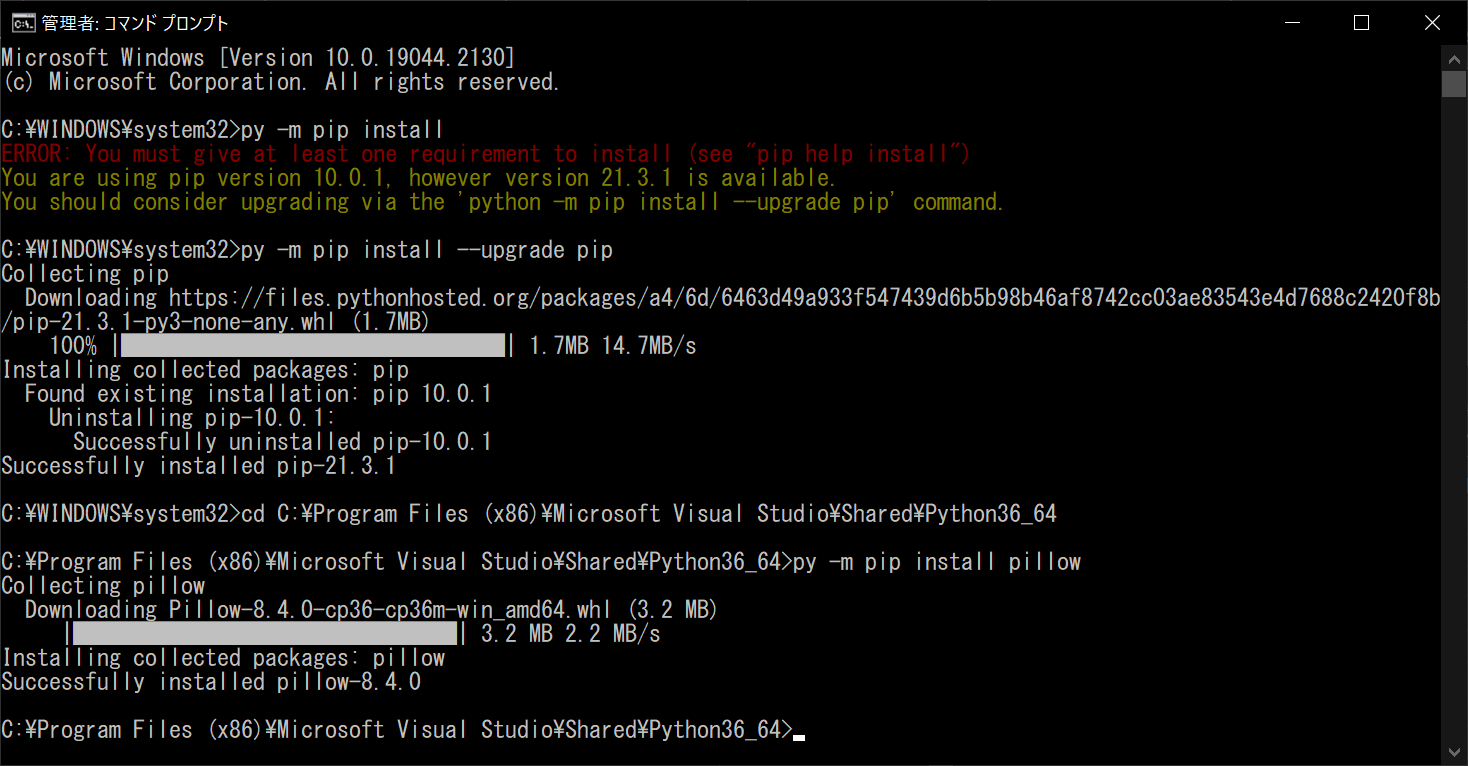
まずは「コマンドプロンプト」を管理者権限で開き、以下のコマンドを入力してください。なおコマンドプロンプトは、タスクバーの検索画面で「cmd」と入力し、一番上に表示されたものを右クリックして「管理者として実行」を選べばOKです。

py -m pip install –upgrade pip

これはPythonのパッケージ「PIP」を、最新バージョンにアップデートするためのものです。アップデートが完了すると、以下の画面のように「Successfully installed pip」と表示されます。

次にVisual StudioのIDEを開き、Pythonで以下のソースコードを実行してください。実行結果として、Python本体の実行ファイルがある場所が表示されます。

import sys
print(sys.executable)

もう一度コマンドプロンプトを管理者権限で開き、以下のコマンドで先ほど確認した「Python.exe」実行ファイルのディレクトリに移動します。

cd C:\Program Files (x86)\Microsoft Visual Studio\Shared\Python36_6

それから以下のコマンドを入力すると、無事にPillow（PIL）のインストールが完了します。

py -m pip install pillow

【応用編】Pillow（PIL）の基本的な使い方

Pillow（PIL）ライブラリの基本的な使い方について、以下3つのポイントに分けて解説します。

Pillow（PIL）で画像を読み込んで行列変数に格納する
PILで読み込んだ画像データをNumPyで「npy形式」で保存する
保存した画像データを読み込んで「png形式」で保存する

Pillow（PIL）で画像を読み込んで行列変数に格納する

まずは、PILライブラリで画像データを読み込み、NumPyの行列変数にデータを格納します。以下の画像をPythonのプロジェクトフォルダ（「pyファイル」があるディレクトリ）に「Sky.png」という名称で保存し、サンプルコードを実行してみましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Sky.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 行列変数の中身を表示する
print(matrix)

//実行結果

PNGファイルの場合、画像データは基本的に4列構成になっており、RGBA（赤、緑、青、アルファ）の順に並んでいます。最小値は0、最大値は255です。アルファチャンネルは画像の不透明度を示し、この値が0に近ければ画像は透明に近くなるので、画像を滑らかに表示したい場合はアルファチャンネルが必要です。また、print関数で画像データの行列を表示する場合、途中の要素は「…」で省略されます。

PILで読み込んだ画像データをNumPyで「npy形式」で保存する

先ほどの手順で読み込んだ画像データを、NumPyライブラリで「npy形式」で保存してみましょう。以下のサンプルコードのように、「save関数」の引数にファイル名と行列変数を指定するだけでOKです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Sky.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 画像データをnpy形式で保存する
numpy.save("Data.npy", matrix)

# 保存完了のメッセージを表示する
print("Data.npyを保存しました！")

//実行結果

なおファイルの拡張子は、「npy」か「npz」でなければエラーになるので注意が必要です。

保存した画像データを読み込んで「png形式」で保存する

NumPyとPILを組み合わせれば、Pythonスクリプトで画像の読み込み&保存が簡単にできます。NumPyの「load関数」で先ほど保存した「npyファイル」を読み込み、PILの「Image.fromarray関数」に行列変数を引き渡すと、再びpngなどの画像データとして復元できます。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Sky.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 画像データをnpy形式で保存する
numpy.save("Data.npy", matrix)

# 保存完了のメッセージを表示する
print("Data.npyを保存しました！")

# 保存した画像データを読み込む
image = numpy.load("Data.npy")

# データを画像情報に復元する
data = Image.fromarray(image)

# png形式で画像を保存する
data.save("Result.png")

# 保存完了のメッセージを表示する
print("Result.pngを保存しました！")

//実行結果

実際に保存した画像と元の画像を比べてみると、まったく同じ内容になっていることが分かります。以上の知識を応用すれば、NumPyとPILで高度な画像編集ができるようになります。

【実践編】NumPyの画像処理テクニック9選！

先ほど紹介した基本的な知識を踏まえて、以下9つの実践的な画像処理テクニックにチャレンジしてみましょう。

画像を拡大縮小して保存する
縮小した画像を横に並べる
赤/緑/青それぞれの単色画像を生成して横方向に結合する
すべての画素値を反転させる「ネガポジ反転」を行う
色数を減らす「減色処理」を行う
白黒のみの「グレースケール」に変換する
ガンマ補正を行う
画像をトリミングする
画像のトリミングと加工/貼り付けを組み合わせる

画像を拡大縮小して保存する

画像の拡大縮小は、「resize関数」の引数に縦横のサイズをタプル形式で指定するだけで行えます。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Sky.png")

# PILライブラリで画像を256*256に縮小する
smallImage = image.resize((256, 256))

# PILライブラリで画像を1024*1024に縮小する
bigImage = image.resize((1024, 1024))

# 縮小した画像データを行列変数に格納する
smallMatrix = numpy.array(smallImage)

# 拡大した画像データを行列変数に格納する
bigMatrix = numpy.array(bigImage)

# 縮小した画像をpng形式で保存する
Image.fromarray(smallMatrix).save("SmallResult.png")

# 拡大した画像をpng形式で保存する
Image.fromarray(bigMatrix).save("BigResult.png")

//実行結果
縮小した画像

拡大した画像

resize関数には、元のアスペクト比とは異なるサイズも設定できます。ちなみに、PILのresize関数の第2引数には、リサンプリングのフィルターも指定できます。選べるフィルターは以下6種類です。

Image.NEAREST
Image.BOX
Image.BILINEAR
Image.HAMMING
Image.BICUBIC
Image.LANCZOS

何も指定しない場合は、デフォルトで「Image.NEAREST」となります。高速に処理できますが、リサンプリングの品質は良くありません。一方、「Image.BICUBIC」や「Image.LANCZOS」は高品質な拡大縮小ができますが、画像処理に時間がかかります。Image.BICUBICでリサイズするサンプルコードを以下に紹介します。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Sky.png")

# PILライブラリで画像を「Image.BICUBIC」フィルタリングで256*256に縮小する
resized = image.resize((256, 256), Image.BICUBIC)

# 縮小した画像データを行列変数に格納する
matrix = numpy.array(resized)

# 縮小した画像をpng形式で保存する
Image.fromarray(matrix).save("Result.png")

//実行結果

縮小した画像を横に並べる

NumPyの「concatenate関数」を活用すると、PILで加工した画像を縦もしくは横方向に、複数並べることができます。concatenate関数の第1引数に、画像データの行列変数をタプル形式で並べるだけでOKです。詳細を以下のサンプルコードで確認しましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Sky.png")

# PILライブラリで画像を256*256に縮小する
image = image.resize((256, 256))

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 5横に並べて結合する
matrix = numpy.concatenate((matrix, matrix, matrix, matrix, matrix), axis = 1)

# 拡大した画像をpng形式で保存する
Image.fromarray(matrix).save("Concatenate.png")

//実行結果

なおconcatenate関数の第2引数には、結合する軸を「0」か「1」で決定します。0の場合は縦方向に、1の場合は横方向の結合となります。今回は1を指定したので、上記のように横方向に画像が並んでいます。

赤/緑/青それぞれの単色画像を生成して横方向に結合する

「単色合成」とは、RGBの成分を1つだけ抽出し、残り2つの成分をすべて0にすることです。1つの色を主体とした画像に加工できます。なお、ここからのサンプルプログラムは、以下の画像を「Flower.png」という名前で保存して実行してください。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 「赤」以外の色の値を0にして、単色画像を生成する
R = matrix.copy() # ディープコピーする
R[:, :, (1, 2)] = 0 # スライスして必要な部分のみ変更する

# 「緑」以外の色の値を0にして、単色画像を生成する
G = matrix.copy() # ディープコピーする
G[:, :, (0, 2)] = 0 # スライスして必要な部分のみ変更する

# 「青」以外の色の値を0にして、単色画像を生成する
B = matrix.copy() # ディープコピーする
B[:, :, (0, 1)] = 0 # スライスして必要な部分のみ変更する

# 画像を横に並べて結合する
matrix = numpy.concatenate((R, G, B), axis = 1)

# 拡大した画像をpng形式で保存する
Image.fromarray(matrix).save("Result.png")

//実行結果

上記のサンプルプログラムでは、赤・緑・青それぞれの色に対して単色画像を作成しています。まずcopy関数で画像データをディープコピーしてから、R[:, :, (1, 2)]、G[:, :, (0, 2)]、B[:, :, (0, 1)]のように、ターゲットの色以外を抽出していることがポイントです。

たとえば赤色の単色合成を行うときは、緑と青の要素を0にする必要があります。画像データは各行の「0番目=赤」「1番目=緑」「2番目=青」と並んでいるため、1番目と2番目を抽出すればOKです。そこでR[:, :, (1, 2)]のように、行列変数から緑と青の要素だけをスライスし、それらすべてを0に置き換えます。

すべての画素値を反転させる「ネガポジ反転」を行う

すべての画素値を反転させる「ネガポジ反転」を行うと、ネガフィルムのような画像を作ることができます。また、元画像が白黒であれば、白と黒が逆になり独特の雰囲気が出ます。詳細を以下のサンプルコードで確認しましょう。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# ネガポジ処理を行う
matrix = 255 - matrix

# 加工した画像をpng形式で保存する
Image.fromarray(matrix).save("Result.png")

//実行結果

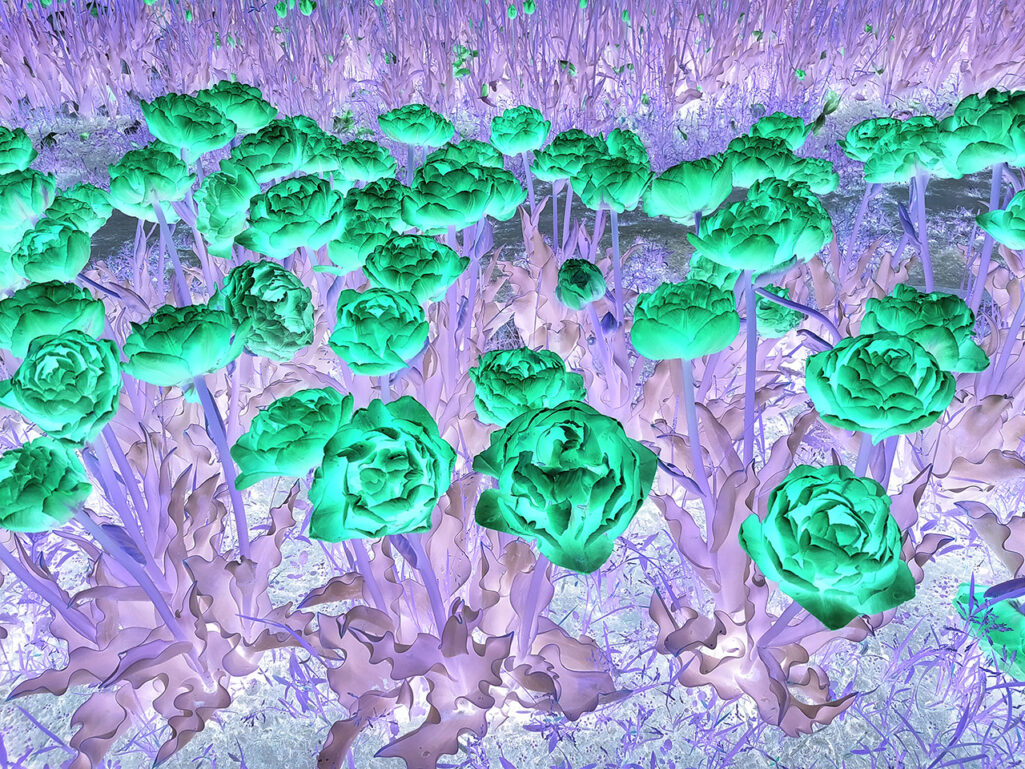
ネガポジ反転のやり方は、単に「matrix = 255 – matrix」のように、すべての画素に対して「最大値 – 画素値」の処理を行うだけです。たとえば元の画素が100の場合、ネガポジ反転を行うと155となります。0の場合は255になるので、完全に色が反転することになります。

色数を減らす「減色処理」を行う

色数を減らす「減色処理」は、「//」演算子で割り算の余りを切り捨てたうえで、同じ値を再度掛け算することで行います。その結果、画素データが少なくなって飛び飛びの値になり、色数を減らすことができます。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 2種類の減色処理を行う
subA = matrix //  64 *  64
subB = matrix // 128 * 128

# オリジナルと合わせて3枚の画像を横並びに結合する
result = numpy.concatenate((matrix, subA, subB), axis = 1)

# 加工した画像をpng形式で保存する
Image.fromarray(result).save("Result.png")

//実行結果

上記のサンプルプログラムのように、減色処理に使う値が大きいほうが、色数が減ってコントラストの強い画像になることが分かります。ダイナミックな画像を作りたい場合に活用してみましょう。

白黒のみの「グレースケール」に変換する

白黒のみの「グレースケール」に画像を変換したいときは、convert関数の引数に「’L’」を指定すると、簡単に白黒画像が作れます。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データをグレースケールに変換して行列変数に格納する
matrix = numpy.array(image.convert('L'))

# 加工した画像をpng形式で保存する
Image.fromarray(matrix).save("Result.png")

//実行結果

上記のサンプルプログラムのように、カラフルな画像を簡単にグレースケールに変換できます。なお白黒画像には、0～255までの256諧調を使う上述のグレースケールと、黒(0)と白(1)の2諧調だけを使う「モノクロ」があります。モノクロの場合は、以下のサンプルコードのようにconvert関数に「’1’」を指定すればOKです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データをグレースケールに変換して行列変数に格納する
matrix = numpy.array(image.convert('1'))

# 加工した画像をpng形式で保存する
Image.fromarray(matrix).save("Result.png")

//実行結果

モノクロにした場合、一般的にディザーと呼ばれる処理が行われて、1種類の色だけで画像が表現されます。まるで版画のようなドットが浮き出た様子が魅力的です。

ガンマ補正を行う

画像の明るさを補正する「ガンマ処理」は、すべての画素を0.0～1.0の浮動小数点値に置き換えたうえで、一定の値を掛け合わせることで行います。ただし計算の結果、行列変数の値が浮動小数点値に変換されるので、画像保存時に再び「uint8型」に戻す必要があります。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 2種類のガンマ補正処理を行う
gammaA = 255.0 * (matrix / 255.0) ** (1 / 2.2)
gammaB = 255.0 * (matrix / 255.0) ** 2.2

# オリジナルと合わせて3枚の画像を横並びに結合する
result = numpy.concatenate((matrix, gammaA, gammaB), axis = 1)

# 加工した画像をpng形式で保存する
Image.fromarray(numpy.uint8(result)).save("Result.png")

//実行結果

画像をトリミングする

画像の一部分だけを抽出したい場合は、行列変数をスライスして、トリミングした部分だけを保存すればOKです。なお、指定するインデックスは「ピクセル座標」と同じですが、画像データは「縦」「横」に並んでいることに注意が必要です。

たとえば、「X = 256ピクセル、Y = 128ピクセル」の部分から「X = 576ピクセル、Y = 320ピクセル」までトリミングしたい場合は、[128:320, 256:576]と指定しないといけません。分かりにくいので、以下のサンプルコードのように、座標とサイズを指定すると自動的にトリミングしてくれる関数を作成すると便利です。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# トリミング用関数を定義する
def trim(array, x, y, width, height):
  return array[y:y + height, x:x + width]

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データを行列変数に格納する
matrix = numpy.array(image)

# 元画像のサイズを表示する
print("元の画像サイズ：{}".format(matrix.shape))

# 任意の場所をX座標256ピクセル・Y座標256ピクセルの位置から、512*512のサイズ分だけトリミングする
trimmed = trim(matrix, 256, 256, 512, 512)

# 元画像のサイズを表示する
print("トリミング後の画像サイズ：{}".format(trimmed.shape))

# 加工した画像をpng形式で保存する
Image.fromarray(trimmed).save("Result.png")

//実行結果

上記のサンプルプログラムでは、実際に画像の一部分をトリミングして保存しましょう。サイズを確認すると、きちんとトリミングできていることが分かります。なお、前述したようにトリミング部分の指定が分かりにくいので、「trim関数」を作成しています。

第1引数にトリミング対象の行列変数、第2・3引数にトリミング開始のX・Y座標値、第4・5引数にトリミングする横幅・高さを指定すると、トリミングした部分の画像データが返るのです。縦と横を逆にしてしまうなどのミスを防げるので、ぜひご活用ください。

画像のトリミングと加工/貼り付けを組み合わせる

これまで紹介してきたテクニックを組み合わせて、画像のトリミングと加工と貼り付けを同時に行ってみましょう。今回は、トリミングした画像を青色と緑色に単色変換したものを、元の画像に貼り合わせています。

//サンプルプログラム

# 「numpy」の機能を使用する
import numpy

# 「PIL」ライブラリの「Image」の機能を使用する
import PIL
from PIL import Image

# トリミング用関数を定義する
def trim(array, x, y, width, height):
  return array[y:y + height, x:x + width]

# PILライブラリで画像を読み込む
image = Image.open("Flower.png")

# 画像データを行列変数に格納する
original = numpy.array(image)

# X座標256ピクセル・Y座標256ピクセルの位置から、512*512のサイズ分だけトリミングする
trimmedA = trim(original, 256, 256, 512, 512)

# X座標512ピクセル・Y座標512ピクセルの位置から、256*256のサイズ分だけトリミングする
trimmedB = trim(original,512, 512, 256, 256)

# 青色の単色画像を作成する
subA = trimmedA.copy()
subA[:, :, (0, 1)] = 0

# 緑色の単色画像を作成する
subB = trimmedB.copy()
subB[:, :, (0, 2)] = 0

# 元画像の任意の場所に、単色画像を張り付ける
original[64:64 + 512, 64:64 + 512] = subA
original[480:480 + 256, 960:960 + 256] = subB

# 加工した画像をpng形式で保存する
Image.fromarray(original).save("Result.png")

//実行結果

重要なポイントは、単色画像を張り付けている部分です。オリジナルの行列変数から、上書きしたい部分をスライスで指定して、単色画像の行列変数を代入すればOKです。ただし、範囲指定した部分のサイズが、上書きする画像のサイズと一致しない場合はエラーが出ます。また、範囲指定は「縦, 横」の順番で行うので、逆にしてしまわないように注意が必要です。