Pythonで「四捨五入」するには？最適な方法や応用テクニックを解説

Pythonで数値を扱うとき、意外と厄介なのが「四捨五入」の処理です。意図せず「切り上げ」や「切り捨て」になってしまい、思うように四捨五入できないことがあります。数値を扱うときは、四捨五入を正確に行わないとトラブルの原因になることがあるので、困ることもあるでしょう。

結論からいうと、Python標準機能の「round関数」では正確な四捨五入ができないことがあるため、「quantize関数」を使うのがおすすめです。本記事では、Pythonで正確に四捨五入を行う方法について、サンプルコード付きで詳しく解説します。

そもそも「四捨五入」とは？Pythonでも概念は同じ！

「四捨五入」とは、対象となる「位（くらい）」の値が「4以下（0, 1, 2, 3, 4）」なら切り捨て、「5以上（5, 6, 7, 8, 9）」なら切り上げることです。

たとえば、「123.456」という数値がある場合、小数点以下を四捨五入すると「123」になります。小数第1位の値が「4」であり、切り捨てる必要があるからです。一方、「234.567」という数値を四捨五入すると、小数第1位の「5」を切り上げるため「235」になります。

実は、Pythonのようなプログラミング言語では、この四捨五入がうまくいかないことが珍しくありません。たとえば、浮動小数点数を四捨五入したいからといって、単に整数型にキャスト（変換）しても望む結果は得られないからです。

//サンプルプログラム

# coding: Shift-JIS

# 浮動小数点数を整数値にキャストする
f1 = 123.456
i1 = int(f1)
print(f"{f1}→{i1}")

# 浮動小数点数を整数値にキャストする
f2 = 123.789
i2 = int(f2)
print(f"{f2}→{i2}")

//実行結果

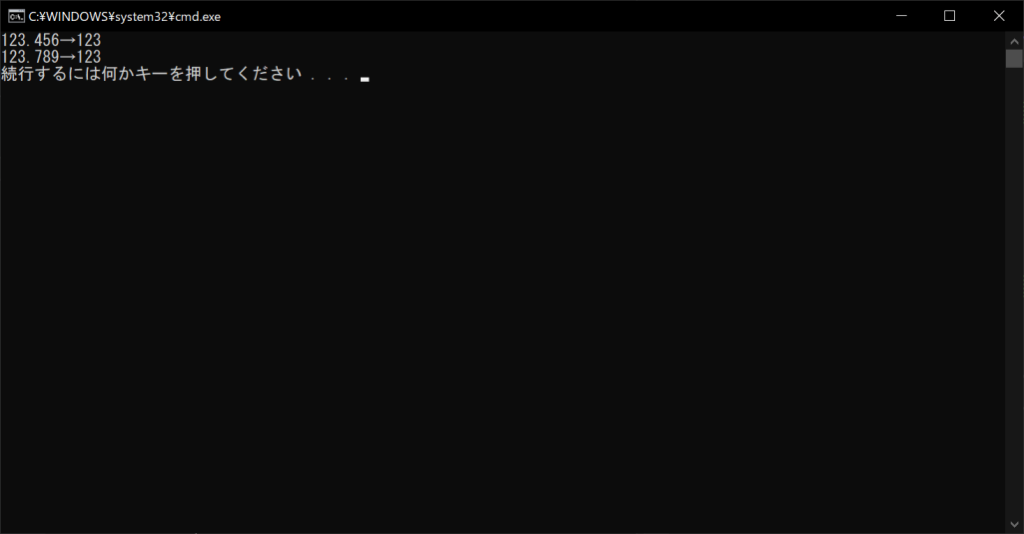
正確な四捨五入を行うと、「123.456」は「123」に、「123.789」は「124」になります。しかし、int型へのキャストは単なる切り捨て処理なので、どちらも「123」になってしまいます。そのため、Pythonで正しい四捨五入を行うためには、専用の関数（メソッド）の使用が必須です。考えられる選択肢として、以下4つの方法を紹介します。

• 選択肢1：組み込み関数の「round」
• 選択肢2：組み込み関数の「format」
• 選択肢3：decimalライブラリ「quantize」
• 選択肢4：独自の「四捨五入」関数・メソッドを実装する

選択肢1：組み込み関数の「round」

Pythonで四捨五入を行うための選択肢として、最初に考えられるのが「round関数」です。roundはPythonの組み込み関数、つまり標準機能として備わっている関数なので、ライブラリをインポートしなくても使えます。round関数について詳しく見ていきましょう。

round関数の基本的な使い方

round関数は、以下2ついずれかの構文で使います。

第1引数のみ指定した場合は、自動的に小数点以下が四捨五入され、結果は整数値になります。一方、第2引数には小数点以下を何桁まで丸めるかを指定し、その下の位が四捨五入されることがポイントです。たとえば、第2引数に「1」を指定した場合は、小数第2位の値が四捨五入され、結果は小数第1位までの浮動小数点数となります。

round関数による四捨五入

実際に、round関数を使用して、浮動小数点数や整数値の四捨五入を行ってみましょう。

//サンプルプログラム

# coding: Shift-JIS

# 浮動小数点数を定義する
f = 123.456789
print(f)

# 第2引数を指定しない → 小数第1位を四捨五入
r = round(f)
print(f"第2引数なしの場合：{f}→{r}")

# 第2引数を「0」にする → 小数第1位を四捨五入
r = round(f, 0)
print(f"第2引数が0の場合：{f}→{r}")

# 第2引数を「1」にする → 小数第2位を四捨五入
r = round(f, 1)
print(f"第2引数が1の場合：{f}→{r}")

# 第2引数を「2」にする → 小数第3位を四捨五入
r = round(f, 2)
print(f"第2引数が2の場合：{f}→{r}")

# 第2引数を「3」にする → 小数第4位を四捨五入
r = round(f, 3)
print(f"第2引数が3の場合：{f}→{r}")

# 第2引数を「4」にする → 小数第5位を四捨五入
r = round(f, 4)
print(f"第2引数が4の場合：{f}→{r}")

# 第2引数を「5」にする → 小数第6位を四捨五入
r = round(f, 5)
print(f"第2引数が5の場合：{f}→{r}")

# 整数値を定義する
i = 123456789
print()
print(i)

# 第2引数を指定しない → 小数第1位を四捨五入
r = round(i)
print(f"第2引数なしの場合：{i}→{r}")

# 第2引数を「-1」にする → 1桁目を四捨五入
r = round(i, -1)
print(f"第2引数が-1の場合：{i}→{r}")

# 第2引数を「-2」にする → 2桁目を四捨五入
r = round(i, -2)
print(f"第2引数が-2の場合：{i}→{r}")

# 第2引数を「-3」にする → 3桁目を四捨五入
r = round(i, -3)
print(f"第2引数が-3の場合：{i}→{r}")

# 第2引数を「-4」にする → 4桁目を四捨五入
r = round(i, -4)
print(f"第2引数が-4の場合：{i}→{r}")

# 第2引数を「-5」にする → 5桁目を四捨五入
r = round(i, -5)
print(f"第2引数が-5の場合：{i}→{r}")

//実行結果

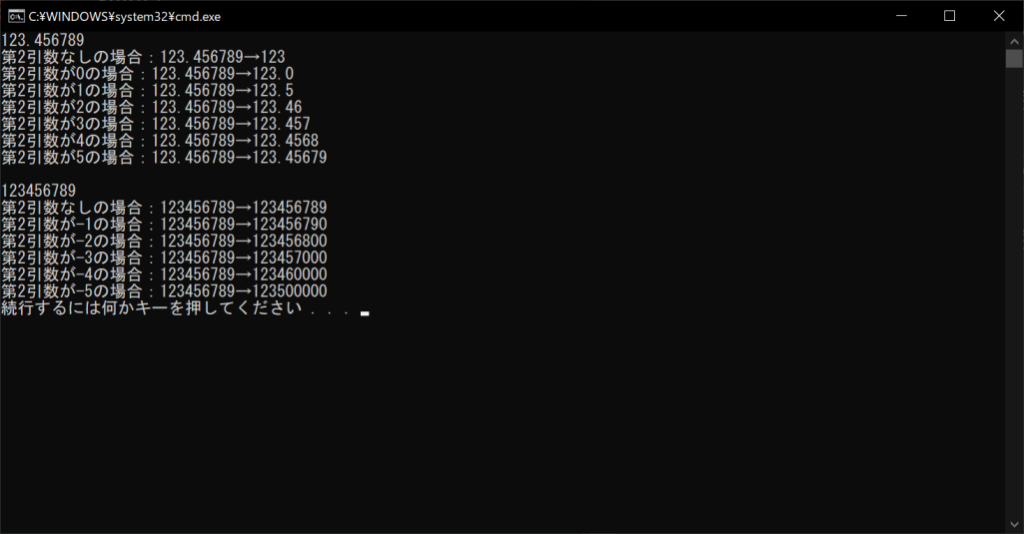
round関数の第2引数に「0」を指定した場合は、第2引数がない場合と同じです。つまり小数第1位が四捨五入されることになり、整数値の場合はそのままになります。第2引数を1増やすたびに、四捨五入される桁は1つずつ下がります。

重要なポイントは、整数値および浮動小数点数の整数部分を四捨五入する際の、第2引数の指定方法です。こちらは第2引数を1減らすたびに、1つ上の桁が四捨五入されます。たとえば、第2引数を「-3」にした場合は、3桁目つまり100の位が四捨五入されるため、上記の実行結果では「123457000」となります。

round関数の注意点｜正確な四捨五入ができないことがある

round関数の注意点は、正確な四捨五入ができないケースがあることです。以下のサンプルコードの実行結果を確認してみましょう。

//サンプルプログラム

# coding: Shift-JIS

print("0.4 → ", round(0.4)) # 「0」になるはず
print("0.5 → ", round(0.5)) # 「1」になるはず
print("0.6 → ", round(0.6)) # 「1」になるはず

print()
print("4 → ", round(4, -1)) # 「0」になるはず
print("5 → ", round(5, -1)) # 「10」になるはず
print("6 → ", round(6, -1)) # 「10」になるはず

print()
print("0.5 → ", round(0.5)) # 「1」になるはず
print("1.5 → ", round(1.5)) # 「2」になるはず
print("2.5 → ", round(2.5)) # 「3」になるはず
print("3.5 → ", round(3.5)) # 「4」になるはず
print("4.5 → ", round(4.5)) # 「5」になるはず

//実行結果

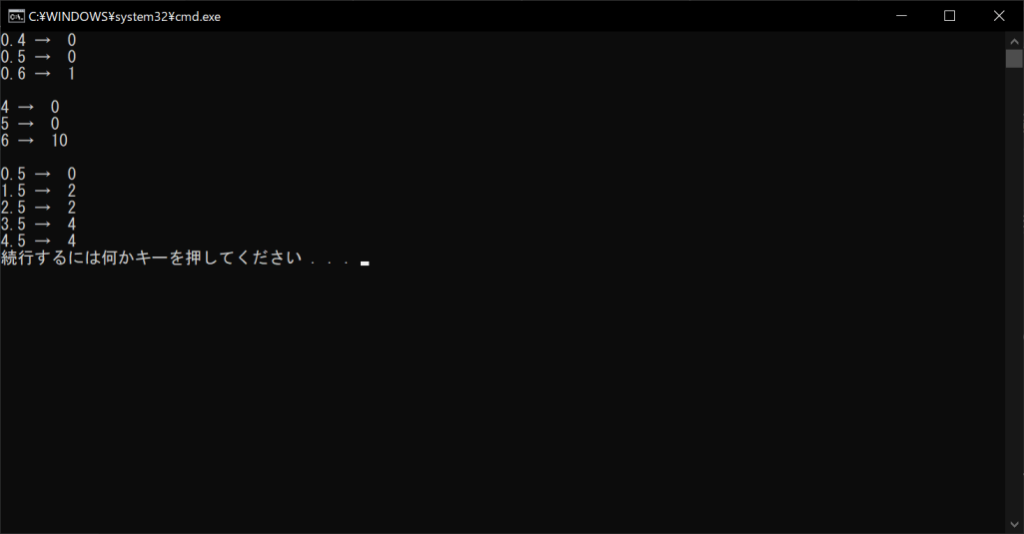
一部の実行結果が想定と異なっています。たとえば、「0.5」を四捨五入すると「1」になるはずですが、round関数の実行結果は「0」になります。同様に、浮動小数点数の場合は、「2.5」が「2」に、「4.5」が「4」になるなど、一部の実行結果が不正確です。

このように、本来「5」は切り上げられるべき値ですが、round関数では切り捨てられてしまうことがあります。その原因は、round関数は一般的な四捨五入ではなく、「銀行家の丸め」を採用しているからです。

「銀行家の丸め」とは？偶数になるほうへ丸める手法

銀行家の丸めは、「5」を四捨五入するときに、結果が偶数になるほうへ丸める手法です。先ほどの実行結果でも、「5」を丸めた結果はすべて偶数になっています。

銀行家の丸めは、「処理」と「丸め」を繰り返したあとに、数値の総合計の誤差が通常の四捨五入より少なくなるというメリットがあります。そのため、正確な処理が求められる金融機関等では、銀行家の丸めが重宝されてきました。しかし、Pythonで数値を取り扱うときは、むしろ思わぬ動作でトラブルが起きる可能性があるので注意が必要です。

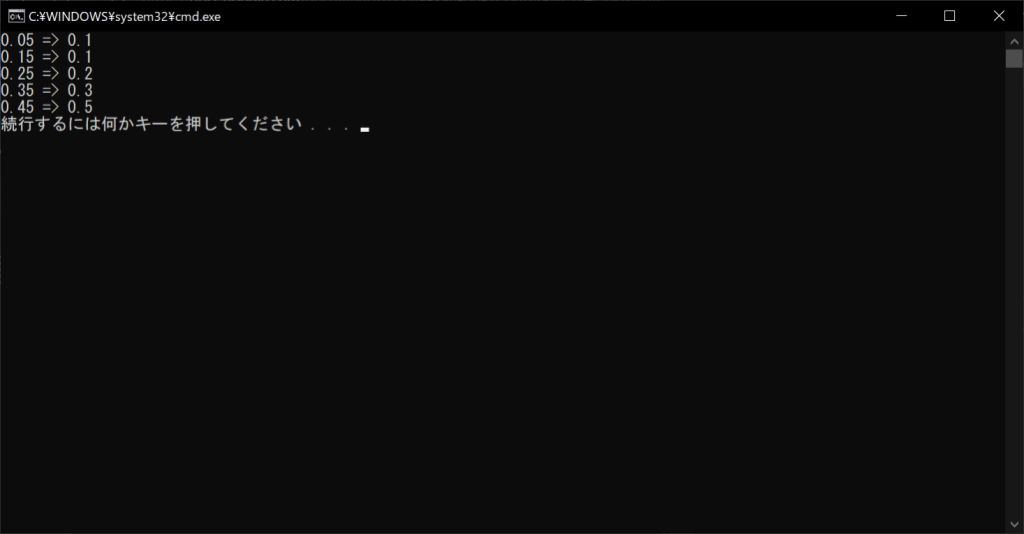
また、以下のように単純に浮動小数点の「精度」が原因で、正確な四捨五入ができないこともあります。コンピューターで浮動小数点数を扱うときは、どうしても精度に限界があり、値によっては誤差が大きくなることがあるからです。

//サンプルプログラム

# coding: Shift-JIS

print('0.05 =>', round(0.05, 1)) # 「0.1」になるはず
print('0.15 =>', round(0.15, 1)) # 「0.2」になるはず
print('0.25 =>', round(0.25, 1)) # 「0.3」になるはず
print('0.35 =>', round(0.35, 1)) # 「0.4」になるはず
print('0.45 =>', round(0.45, 1)) # 「0.5」になるはず

//実行結果

選択肢2：組み込み関数の「format」

round関数と同じく、組み込み関数で簡単に使えるのが「format関数」です。format関数は、主に指定のフォーマットに従って文字列を作成するためのものですが、数値を四捨五入するためにも使えます。

format関数の基本的な使い方

format関数は、以下2ついずれかの構文で使います。

「桁数」の部分には、表示する桁数を指定します。たとえば、小数第2位を四捨五入したい場合は、小数第1位まで表示することになるため「.1f」と指定すればOKです。ただし、round関数とは異なり、format関数では整数部分の四捨五入を行うことはできません。

format関数による四捨五入

実際に、format関数を使用して、浮動小数点数の四捨五入を行ってみましょう。

//サンプルプログラム

# coding: Shift-JIS

# 浮動小数点数を定義する
f = 123.456789
print(f)

# フォーマットを「.0f」にする → 小数第1位を四捨五入
r = format(f, ".0f")
print(f"フォーマットが「.0f」の場合：{f}→{r}")

# フォーマットを「.1f」にする → 小数第2位を四捨五入
r = format(f, ".1f")
print(f"フォーマットが「.1f」の場合：{f}→{r}")

# フォーマットを「.2f」にする → 小数第3位を四捨五入
r = format(f, ".2f")
print(f"フォーマットが「.2f」の場合：{f}→{r}")

# フォーマットを「.3f」にする → 小数第4位を四捨五入
r = format(f, ".3f")
print(f"フォーマットが「.3f」の場合：{f}→{r}")

# フォーマットを「.4f」にする → 小数第5位を四捨五入
r = format(f, ".4f")
print(f"フォーマットが「.4f」の場合：{f}→{r}")

# フォーマットを「.5f」にする → 小数第6位を四捨五入
r = format(f, ".5f")
print(f"フォーマットが「.5f」の場合：{f}→{r}")

//実行結果

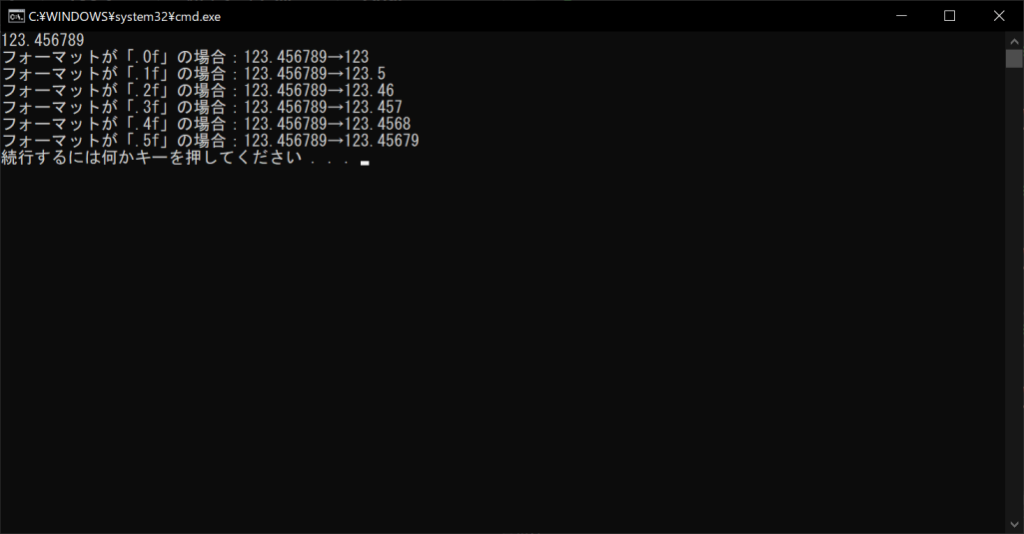
format関数の注意点｜「銀行家の丸め」を採用していることなど

先ほどのround関数と同じく、「銀行家の丸め」を採用しているため、以下のように偶数になるように丸められてしまうケースがあります。

//サンプルプログラム

# coding: Shift-JIS

print("0.4 → ", format(0.4, ".0f")) # 「0」になるはず
print("0.5 → ", format(0.5, ".0f")) # 「1」になるはず
print("0.6 → ", format(0.6, ".0f")) # 「1」になるはず

print()
print("0.5 → ", format(0.5, ".0f")) # 「1」になるはず
print("1.5 → ", format(1.5, ".0f")) # 「2」になるはず
print("2.5 → ", format(2.5, ".0f")) # 「3」になるはず
print("3.5 → ", format(3.5, ".0f")) # 「4」になるはず
print("4.5 → ", format(4.5, ".0f")) # 「5」になるはず

//実行結果

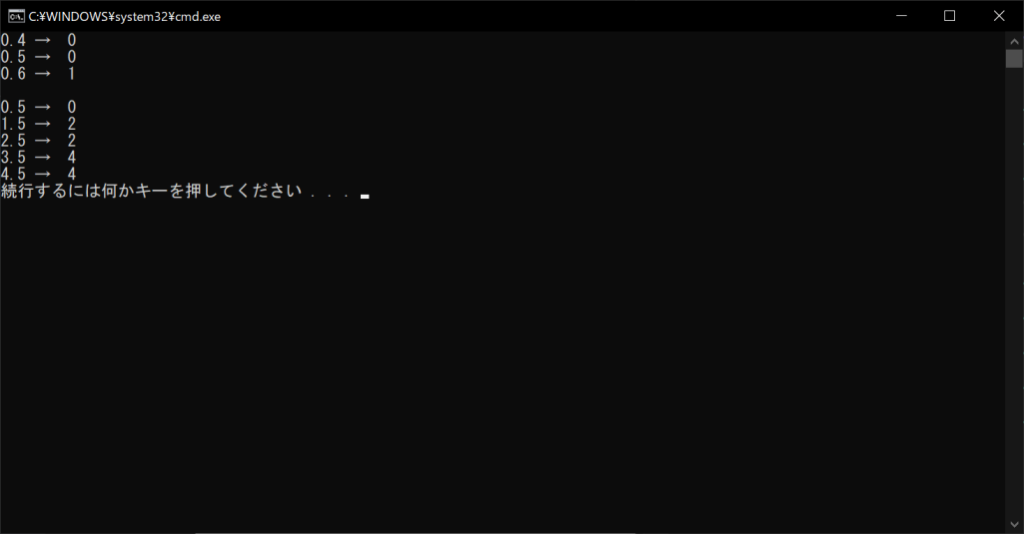
また、format関数は小数点以下の桁しか四捨五入できないため、整数値や浮動小数点数の整数部分の四捨五入はできません。さらに、format関数は結果を「文字列」で返すため、再度計算に使う場合は数値型にキャスト（変換）する必要があるのです。format関数は制約が多いため、基本的にはround関数のほうが使い勝手が良いといえるでしょう。

選択肢3：decimalライブラリ「quantize」

decimalライブラリの「quantize関数」は、Pythonで四捨五入を正確に行うための最も現実的な選択肢です。前述したround関数やformat関数のデメリットも、quantize関数であれば解消できます。

quantize関数の基本的な使い方

quantize関数を使用するためには、まず以下のようにdecimalライブラリをインポートする必要があります。

このとき、「丸めモード」の定数もインポートする必要があります。丸めモードには、「ROUND_HALF_UP」と「ROUND_HALF_EVEN」の2種類があり、前者は通常の四捨五入・後者は銀行家の丸めです。

丸めモードは、後述するquantize関数の引数で指定しますが、銀行家の丸めは基本的に使わないので、ROUND_HALF_UPのみインポートすればOKです。次に、以下の手順でDecimalオブジェクトを作成しましょう。

Decimalのコンストラクタの引数には、四捨五入したい数値を「文字列」に変換してから引き渡すことが重要です。前述したように、Pythonの浮動小数点数には誤差があります。文字列としてDecimalオブジェクトに引き渡すことで、誤差を吸収して正確な処理ができるようになります。最後に、以下のようにquantize関数を使用し、数値を四捨五入しましょう。

先ほど生成したDecimal変数の「quantize関数」を呼び出し、「フォーマット」と「丸めモード」を設定します。フォーマットは、「”0″」「”0.1″」「”0.01″」などのように、表示したい桁数を指定することがポイントです。たとえば、「”0.1″」の場合は小数第1位まで表示するので、小数第2位を四捨五入することになります。

整数部分を四捨五入する場合は、「”1E1″」や「”1E3″」のような「指数表記」が必要です。「”1E2″」とすると、2桁目つまり10の位が四捨五入されます。ただし、この場合は結果も指数表記となるので、int型にキャストするほうが無難です。

引数の「rounding」については、基本的に「ROUND_HALF_UP」を指定します。「ROUND_HALF_EVEN」にすると、銀行家の丸めとなり、round関数やformat関数のような不正確な四捨五入となるため注意が必要です。

quantize関数による四捨五入

実際に、quantize関数を使用して、浮動小数点数や整数値の四捨五入を行ってみましょう。詳細は以下のサンプルコードのとおりです。

//サンプルプログラム

# coding: Shift-JIS

# decimalライブラリをインポートし、通常の四捨五入モードに設定する
from decimal import Decimal, ROUND_HALF_UP

# 浮動小数点数を定義する
f = 123.456789
print(f)

# Decimalオブジェクトを生成する
d = Decimal(str(f))

# フォーマットに「0」を指定する => 小数第1位を四捨五入
r = d.quantize(Decimal("0"), rounding = ROUND_HALF_UP)
print(f"フォーマットに「0」を指定した場合：{f}→{r}")

# フォーマットに「0.1」を指定する => 小数第2位を四捨五入
r = d.quantize(Decimal("0.1"), rounding = ROUND_HALF_UP)
print(f"フォーマットに「0.1」を指定した場合：{f}→{r}")

# フォーマットに「0.01」を指定する => 小数第3位を四捨五入
r = d.quantize(Decimal("0.01"), rounding = ROUND_HALF_UP)
print(f"フォーマットに「0.01」を指定した場合：{f}→{r}")

# フォーマットに「0.001」を指定する => 小数第4位を四捨五入
r = d.quantize(Decimal("0.001"), rounding = ROUND_HALF_UP)
print(f"フォーマットに「0.001」を指定した場合：{f}→{r}")

# フォーマットに「0.0001」を指定する => 小数第5位を四捨五入
r = d.quantize(Decimal("0.0001"), rounding = ROUND_HALF_UP)
print(f"フォーマットに「0.0001」を指定した場合：{f}→{r}")

# フォーマットに「0.00001」を指定する => 小数第6位を四捨五入
r = d.quantize(Decimal("0.00001"), rounding = ROUND_HALF_UP)
print(f"フォーマットに「0.00001」を指定した場合：{f}→{r}")

# 整数値を定義する
i = 123456789
print()
print(i)

# Decimalオブジェクトを生成する
d = Decimal(str(i))

# フォーマットに「1E1」を指定する => 1桁目を四捨五入
r = int(d.quantize(Decimal("1E1"), rounding = ROUND_HALF_UP))
print(f"フォーマットに「1E1」を指定した場合：{i}→{r}")

# フォーマットに「1E2」を指定する => 2桁目を四捨五入
r = int(d.quantize(Decimal("1E2"), rounding = ROUND_HALF_UP))
print(f"フォーマットに「1E2」を指定した場合：{i}→{r}")

# フォーマットに「1E3」を指定する => 3桁目を四捨五入
r = int(d.quantize(Decimal("1E3"), rounding = ROUND_HALF_UP))
print(f"フォーマットに「1E3」を指定した場合：{i}→{r}")

# フォーマットに「1E4」を指定する => 4桁目を四捨五入
r = int(d.quantize(Decimal("1E4"), rounding = ROUND_HALF_UP))
print(f"フォーマットに「1E4」を指定した場合：{i}→{r}")

# フォーマットに「1E5」を指定する => 5桁目を四捨五入
r = int(d.quantize(Decimal("1E5"), rounding = ROUND_HALF_UP))
print(f"フォーマットに「1E5」を指定した場合：{i}→{r}")

# フォーマットに「1E6」を指定する => 6桁目を四捨五入
r = int(d.quantize(Decimal("1E6"), rounding = ROUND_HALF_UP))
print(f"フォーマットに「1E6」を指定した場合：{i}→{r}")

//実行結果

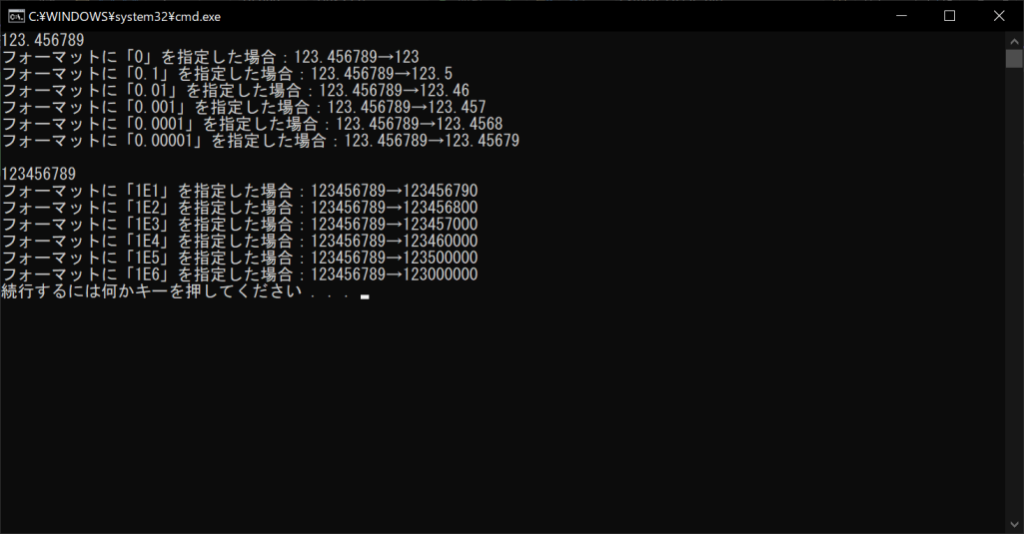
フォーマットの指定方法がわかりにくいですが、小数点以下を四捨五入する場合は、「0」「0.1」「0.01」のように、下の桁になるほどフォーマットの数値も小さくすればOKです。一方で、整数部分を四捨五入する場合は「1E1」「1E2」「1E3」のように、「1E」のあとに四捨五入する桁数を指定しましょう。

関数の魅力｜どのような場合でも正確な四捨五入ができる

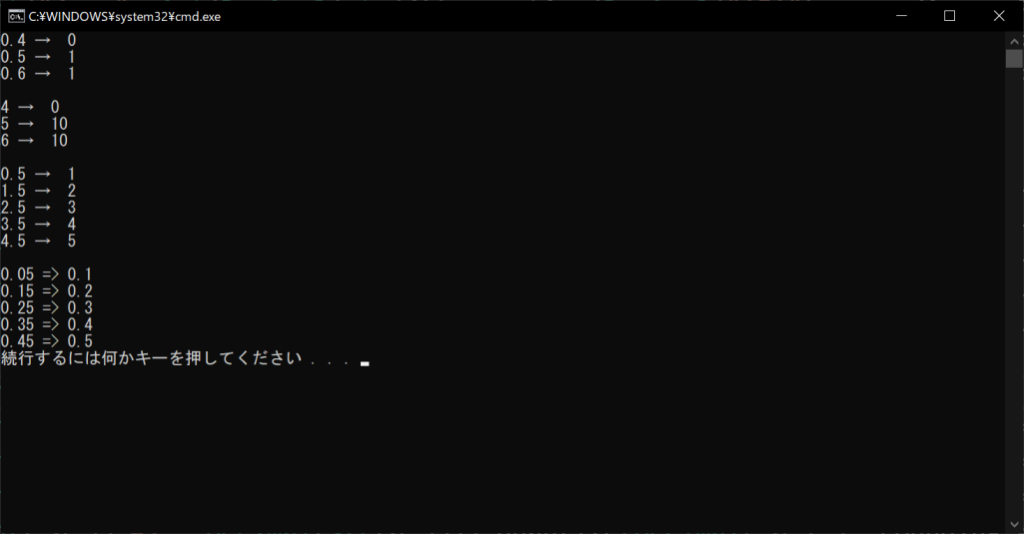
quantize関数で実行されるのは、「銀行家の丸め」ではなく通常の四捨五入なので、どのようなときでも正しい結果が得られます。さらに、浮動小数点数ではなく文字列の状態で四捨五入の処理を行うため、round関数のときのような「誤差」による誤りもありません。詳細を以下のサンプルコードで確認してみましょう。

//サンプルプログラム

# coding: Shift-JIS

# decimalライブラリをインポートし、通常の四捨五入モードに設定する
from decimal import Decimal, ROUND_HALF_UP

print("0.4 → ", Decimal(str(0.4)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「0」になるはず
print("0.5 → ", Decimal(str(0.5)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「1」になるはず
print("0.6 → ", Decimal(str(0.6)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「1」になるはず

print()
print("4 → ", int(Decimal(str(4)).quantize(Decimal("1E1"), rounding = ROUND_HALF_UP))) # 「0」になるはず
print("5 → ", int(Decimal(str(5)).quantize(Decimal("1E1"), rounding = ROUND_HALF_UP))) # 「10」になるはず
print("6 → ", int(Decimal(str(6)).quantize(Decimal("1E1"), rounding = ROUND_HALF_UP))) # 「10」になるはず

print()
print("0.5 → ", Decimal(str(0.5)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「1」になるはず
print("1.5 → ", Decimal(str(1.5)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「2」になるはず
print("2.5 → ", Decimal(str(2.5)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「3」になるはず
print("3.5 → ", Decimal(str(3.5)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「4」になるはず
print("4.5 → ", Decimal(str(4.5)).quantize(Decimal("0"), rounding = ROUND_HALF_UP)) # 「5」になるはず

print()
f = 0.05
print('0.05 =>', Decimal(str(f)).quantize(Decimal("0.1"), rounding = ROUND_HALF_UP)) # 「0.1」になるはず
f = 0.15
print('0.15 =>', Decimal(str(f)).quantize(Decimal("0.1"), rounding = ROUND_HALF_UP)) # 「0.2」になるはず
f = 0.25
print('0.25 =>', Decimal(str(f)).quantize(Decimal("0.1"), rounding = ROUND_HALF_UP)) # 「0.3」になるはず
f = 0.35
print('0.35 =>', Decimal(str(f)).quantize(Decimal("0.1"), rounding = ROUND_HALF_UP)) # 「0.4」になるはず
f = 0.45
print('0.45 =>', Decimal(str(f)).quantize(Decimal("0.1"), rounding = ROUND_HALF_UP)) # 「0.5」になるはず

//実行結果

選択肢4：独自の「四捨五入」関数・メソッドを実装する

これまでは、Pythonの標準機能やライブラリに搭載されている、公式の関数やメソッドについて解説してきました。しかし、Pythonはプログラミング言語なので、クリエイティブな処理ができます。そのため、以下のような関数を独自に実装することでも、先ほどのquantize関数と同じような結果が得られます。

# mathライブラリを使用する
import math

# オリジナルの四捨五入関数を定義する
def original_round(value, digit = 0):
# 桁数と符合を算出する
power = 10 ** digit
sign = math.copysign(1, value)

# 四捨五入の処理を行う
rounded = (sign * value * power * 2 + 1) // 2
rounded /= power * sign

# 小数第1位以上の桁を四捨五入する場合は整数値に変換する
if digit <= 0:
rounded = int(rounded)

return rounded

重要なポイントは引数「digit」の指定方法で、「0」「1」「2」のように、小数点以下の表示桁数を指定するだけでOKです。つまり、「1」の場合は小数第2位、「2」の場合は小数第3位が四捨五入されます。一方、整数部分を四捨五入する場合は、「-1」「-2」「-3」のように、四捨五入したい桁数に「マイナス」をつけます。

なお、オリジナル関数内で「math.copysign関数」を使用していますが、これは対象となる数値の符号を取得するためのものです。四捨五入の処理時にこの符号を反映させることで、マイナスの値の四捨五入も正確に行えるようになります。

オリジナルの関数による四捨五入

実際に、オリジナルの関数・メソッドを使用して、浮動小数点数や整数値の四捨五入を行ってみましょう。

//サンプルプログラム

# coding: Shift-JIS

# mathライブラリを使用する
import math

# オリジナルの四捨五入関数を定義する
def original_round(value, digit = 0):
  # 桁数と符合を算出する
  power = 10 ** digit
  sign = math.copysign(1, value)

  # 四捨五入の処理を行う
  rounded = (sign * value * power * 2 + 1) // 2
  rounded /= power * sign

  # 小数第1位以上の桁を四捨五入する場合は整数値に変換する
  if digit <= 0: rounded = int(rounded) return rounded # 浮動小数点数を定義する f = 123.456789 print(f) # フォーマットに「0」を指定する => 小数第1位を四捨五入
r = original_round(f, 0)
print(f"フォーマットに「0」を指定した場合：{f}→{r}")

# フォーマットに「1」を指定する => 小数第2位を四捨五入
r = original_round(f, 1)
print(f"フォーマットに「1」を指定した場合：{f}→{r}")

# フォーマットに「2」を指定する => 小数第3位を四捨五入
r = original_round(f, 2)
print(f"フォーマットに「2」を指定した場合：{f}→{r}")

# フォーマットに「3」を指定する => 小数第4位を四捨五入
r = original_round(f, 3)
print(f"フォーマットに「3」を指定した場合：{f}→{r}")

# フォーマットに「4」を指定する => 小数第5位を四捨五入
r = original_round(f, 4)
print(f"フォーマットに「4」を指定した場合：{f}→{r}")

# フォーマットに「5」を指定する => 小数第6位を四捨五入
r = original_round(f, 5)
print(f"フォーマットに「5」を指定した場合：{f}→{r}")

# 整数値を定義する
i = 123456789
print()
print(i)

# フォーマットに「-1」を指定する => 1桁目を四捨五入
r = original_round(i, -1)
print(f"フォーマットに「-1」を指定した場合：{i}→{r}")

# フォーマットに「-2」を指定する => 2桁目を四捨五入
r = original_round(i, -2)
print(f"フォーマットに「-2」を指定した場合：{i}→{r}")

# フォーマットに「-3」を指定する => 3桁目を四捨五入
r = original_round(i, -3)
print(f"フォーマットに「-3」を指定した場合：{i}→{r}")

# フォーマットに「-4」を指定する => 4桁目を四捨五入
r = original_round(i, -4)
print(f"フォーマットに「-4」を指定した場合：{i}→{r}")

//実行結果

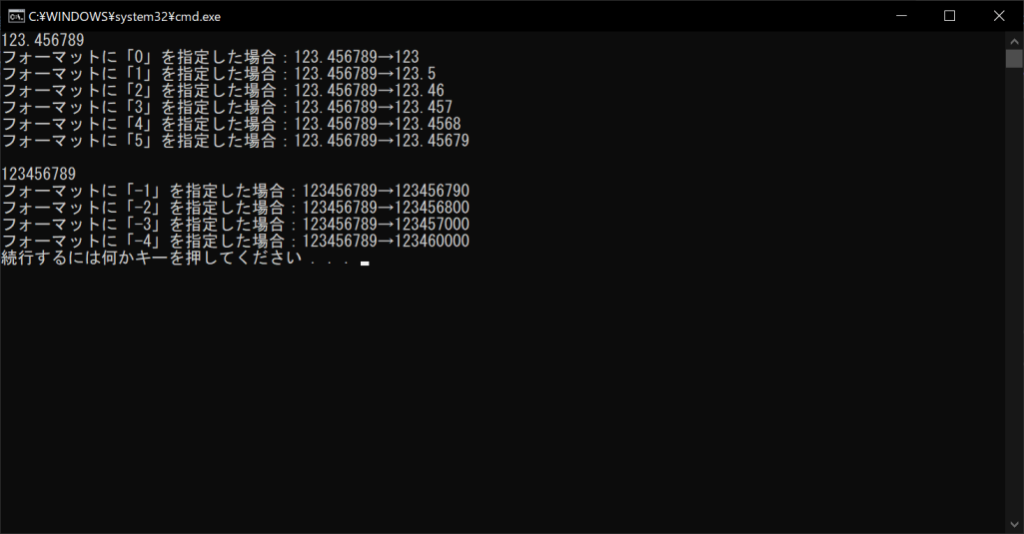
前述した「quantize関数」と異なり、オブジェクトの作成や文字列型への変換が必要なく、フォーマット指定も簡単なので使いやすいことが魅力です。自作関数を定義する手間はかかりますが、quantize関数より直感的に使いやすいといえるでしょう。

オリジナル関数の魅力｜簡単に使えるうえに演算結果が基本的に正確

今回ご紹介したオリジナル関数は、quantize関数より簡単に使えるうえに、round関数やformat関数より正確な四捨五入ができることが魅力です。実際に以下のサンプルコードで、四捨五入の精度を調べてみましょう。

//サンプルプログラム

# coding: Shift-JIS

# mathライブラリを使用する
import math

# オリジナルの四捨五入関数を定義する
def original_round(value, digit = 0):
  # 桁数と符合を算出する
  power = 10 ** digit
  sign = math.copysign(1, value)

  # 四捨五入の処理を行う
  rounded = (sign * value * power * 2 + 1) // 2
  rounded /= power * sign

  # 小数第1位以上の桁を四捨五入する場合は整数値に変換する
  if digit <= 0: rounded = int(rounded) return rounded print() print("4 → ", original_round(4, -1)) # 「0」になるはず print("5 → ", original_round(5, -1)) # 「10」になるはず print("6 → ", original_round(6, -1)) # 「10」になるはず print() print("0.5 → ", original_round(0.5, 0)) # 「1」になるはず print("1.5 → ", original_round(1.5, 0)) # 「2」になるはず print("2.5 → ", original_round(2.5, 0)) # 「3」になるはず print("3.5 → ", original_round(3.5, 0)) # 「4」になるはず print("4.5 → ", original_round(4.5, 0)) # 「5」になるはず print() print('0.05 =>', original_round(0.05, 1)) # 「0.1」になるはず
print('0.15 =>', original_round(0.15, 1)) # 「0.2」になるはず
print('0.25 =>', original_round(0.25, 1)) # 「0.3」になるはず
print('0.35 =>', original_round(0.35, 1)) # 「0.4」になるはず
print('0.45 =>', original_round(0.45, 1)) # 「0.5」になるはず

print()
print('-0.5 =>', original_round(-0.5, 0)) # 「-1」になるはず
print('-1.5 =>', original_round(-1.5, 0)) # 「-2」になるはず
print('-2.5 =>', original_round(-2.5, 0)) # 「-3」になるはず
print('-3.5 =>', original_round(-3.5, 0)) # 「-4」になるはず
print('-4.5 =>', original_round(-4.5, 0)) # 「-5」になるはず

//実行結果

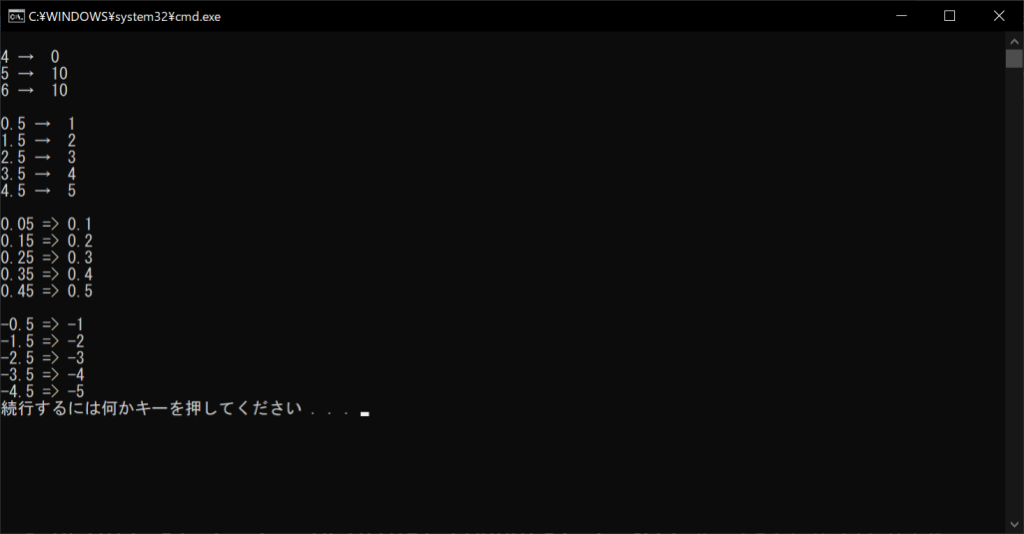
ただし、オリジナル関数は浮動小数点数をそのまま扱っているため、計算誤差が出るケースはあります。そのため、可能な限り正確な四捨五入をしたい場合は、quantize関数のほうが良いです。ただし、quantize関数は扱いが面倒な部分があるので、正確さと手軽さのバランスを求めるなら、自作関数も有力な候補となるでしょう。

「切り捨て」を行う方法

ここまでは四捨五入を行う関数・メソッドについて解説してきましたが、「切り捨て」を行う方法についても見ていきましょう。

• int関数｜0に近づく切り捨て
• quantize関数のROUND_DOWNモード｜0に近づく切り捨て
• math.floor関数｜負の無限大に近づく切り捨て
• quantize関数のROUND_FLOORモード｜負の無限大に近づく切り捨て

int関数｜0に近づく切り捨て

int関数は、浮動小数点数などをint型つまり整数値に変換するためのメソッドです。値が正の場合も負の場合も、0に近づく切り捨てが行われます。

//サンプルプログラム

# coding: Shift-JIS

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「int関数」で切り捨てる
# この方法では「0に近づく切り捨て」が行われる
r1 = int(f1)
r2 = int(f2)
r3 = int(f3)
r4 = int(f4)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

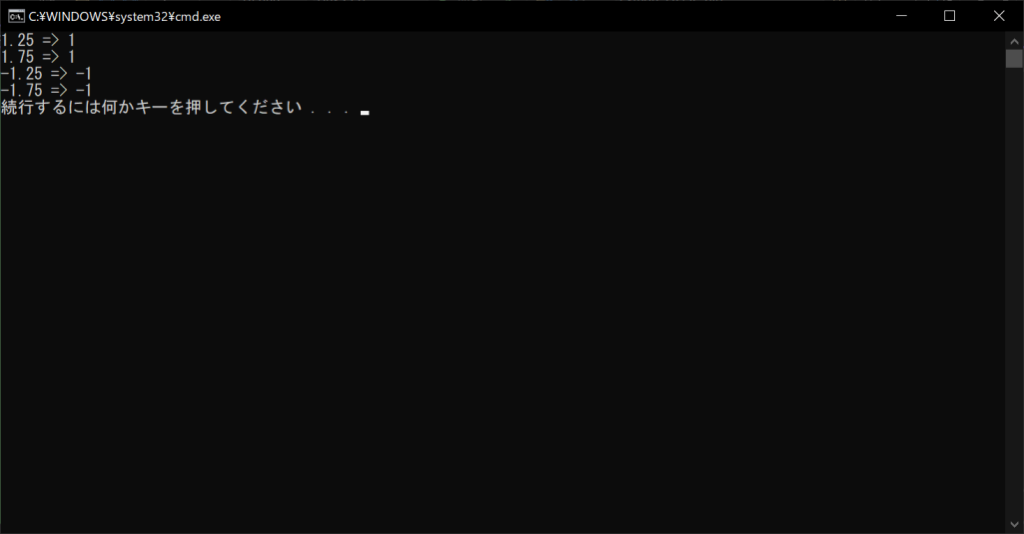
「-1.25」や「-1.75」の切り捨て結果が、「-2」ではなく「-1」になっていることがポイントです。これは、0に近づく切り捨てが行われることが理由です。つまり、数値が正の場合は値が小さくなる方向に、負の場合は大きくなる方向に切り捨てが行われます。

quantize関数のROUND_DOWNモード｜0に近づく切り捨て

先ほど紹介したquantize関数は、「ROUND_DOWN」モードを指定すると、以下のように0に近づく切り捨てができます。

//サンプルプログラム

# coding: Shift-JIS

# decimalライブラリを使用する
from decimal import Decimal, ROUND_DOWN

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「quantize関数」で切り捨てる
# この方法では「0に近づく切り捨て」が行われる
r1 = Decimal(f1).quantize(Decimal("0"), rounding = ROUND_DOWN)
r2 = Decimal(f2).quantize(Decimal("0"), rounding = ROUND_DOWN)
r3 = Decimal(f3).quantize(Decimal("0"), rounding = ROUND_DOWN)
r4 = Decimal(f4).quantize(Decimal("0"), rounding = ROUND_DOWN)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

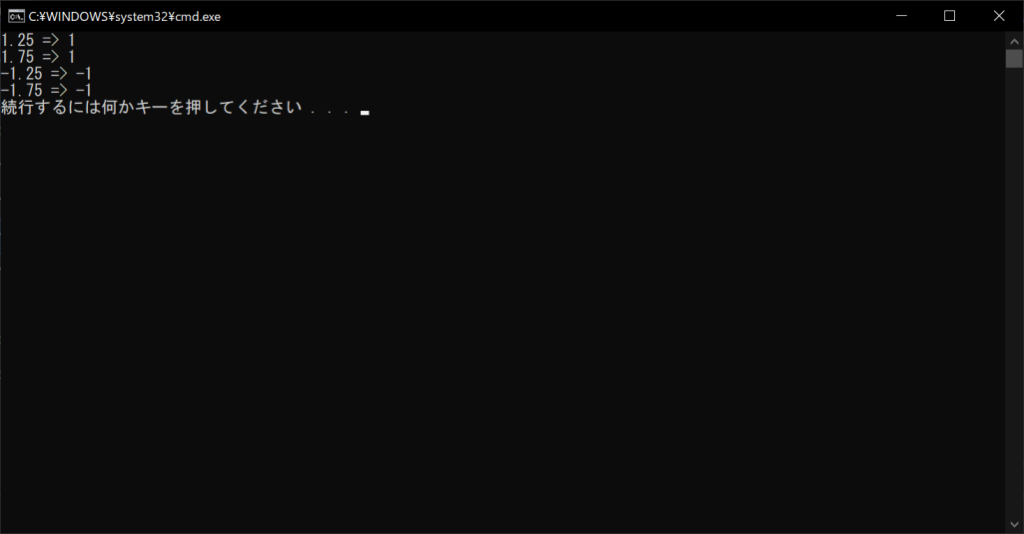
実行結果は先ほどのint関数と同じです。いずれの場合も絶対値が小さくなる方向に切り捨てが行われます。

math.floor関数｜負の無限大に近づく切り捨て

mathライブラリの「floor関数」を使うと、負の無限大に近づく切り捨てができます。つまり、値が正の場合も負の場合も、値が小さくなる方向に切り捨てが行われるということです。

//サンプルプログラム

# coding: Shift-JIS

# mathライブラリを使用する
import math

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「math.floor関数」で切り捨てる
# この方法では「負の無限大に近づく切り捨て」が行われる
r1 = math.floor(f1)
r2 = math.floor(f2)
r3 = math.floor(f3)
r4 = math.floor(f4)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

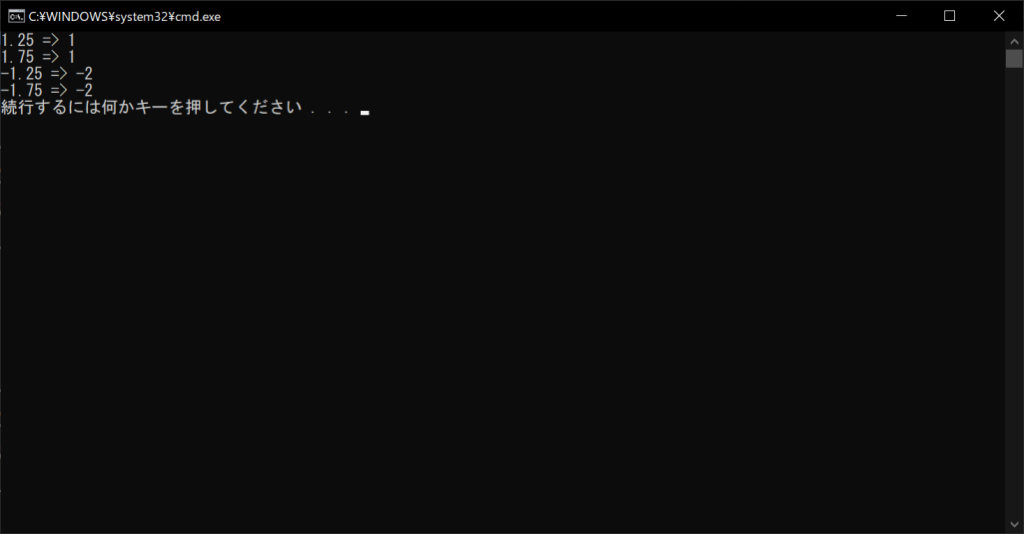
「-1.25」や「-1.75」の切り捨て結果が、「-2」になっていることがポイントです。これは、負の無限大に近づく方向に切り捨てられることが理由です。

quantize関数のROUND_FLOORモード｜負の無限大に近づく切り捨て

quantize関数を「ROUND_FLOOR」モードで使用すると、以下のように負の無限大に近づく切り捨てができます。

//サンプルプログラム

# coding: Shift-JIS

# decimalライブラリを使用する
from decimal import Decimal, ROUND_FLOOR

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「quantize関数」で切り捨てる
# この方法では「負の無限大に近づく切り捨て」が行われる
r1 = Decimal(f1).quantize(Decimal("0"), rounding = ROUND_FLOOR)
r2 = Decimal(f2).quantize(Decimal("0"), rounding = ROUND_FLOOR)
r3 = Decimal(f3).quantize(Decimal("0"), rounding = ROUND_FLOOR)
r4 = Decimal(f4).quantize(Decimal("0"), rounding = ROUND_FLOOR)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

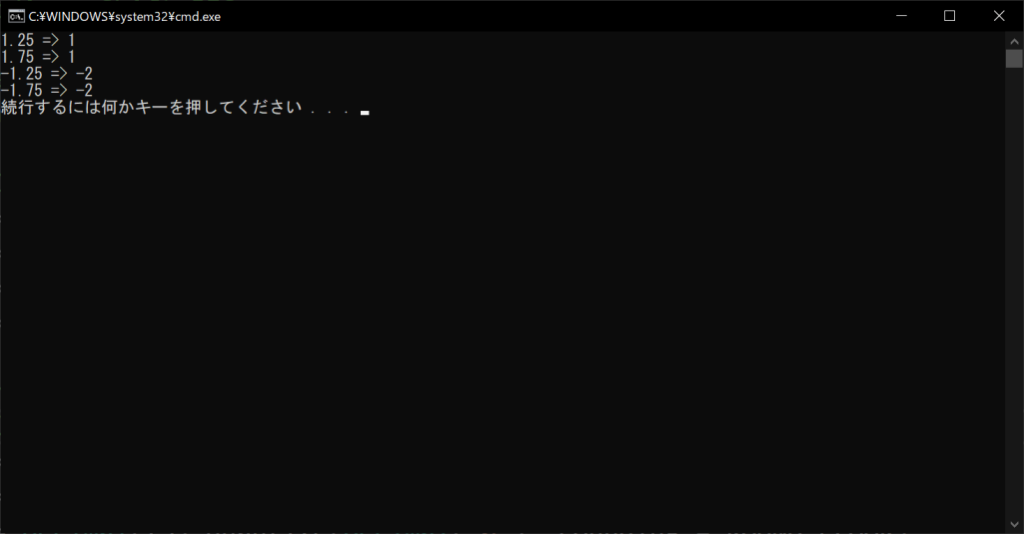
先ほどの「math.floor関数」と同じく、値の符号に関係なく値が小さくなる方向に切り捨てが行われます。

「切り上げ」を行う方法

ここからは、「切り上げ」を行う方法について、以下3つの関数・メソッドの使い方を見ていきましょう。

• quantize関数のROUND_UPモード｜0から遠ざかる切り上げ
• math.ceil関数｜正の無限大に近づく切り上げ
• quantize関数のROUND_CEILINGモード｜正の無限大に近づく切り上げ

quantize関数のROUND_UPモード｜0から遠ざかる切り上げ

quantize関数を「ROUND_UP」モードで使用すると、0から遠ざかる切り捨てが行われます。正の値も負の値も、絶対値が大きくなる方向に切り捨てが行われることが特徴です。

//サンプルプログラム

# coding: Shift-JIS

# decimalライブラリを使用する
from decimal import Decimal, ROUND_UP

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「quantize関数」で切り上げる
# この方法では「0から遠ざかる切り上げ」が行われる
r1 = Decimal(f1).quantize(Decimal("0"), rounding = ROUND_UP)
r2 = Decimal(f2).quantize(Decimal("0"), rounding = ROUND_UP)
r3 = Decimal(f3).quantize(Decimal("0"), rounding = ROUND_UP)
r4 = Decimal(f4).quantize(Decimal("0"), rounding = ROUND_UP)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

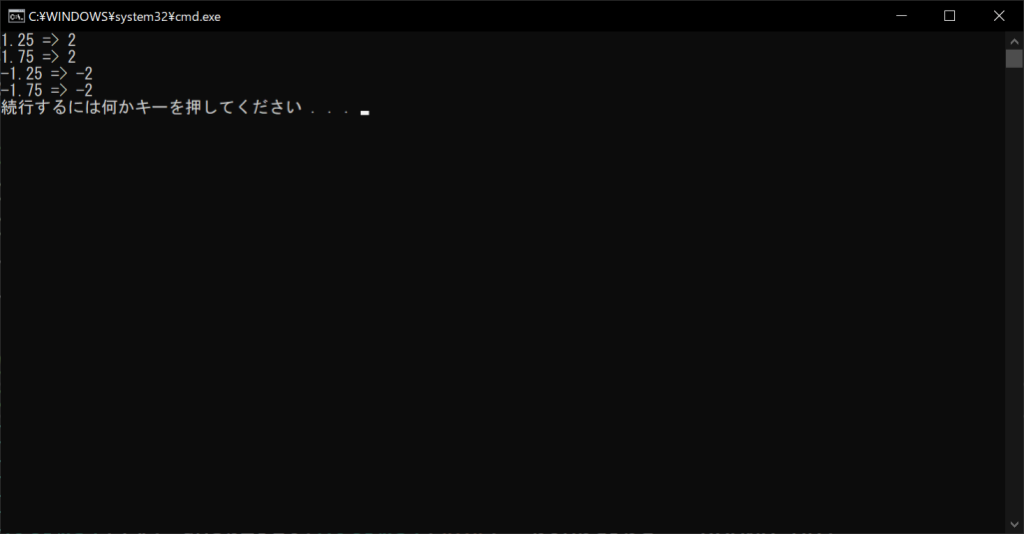
「-1.25」や「-1.75」の切り上げ結果が、「-1」ではなく「-2」になっていることがポイントです。これは、0から遠ざかる切り捨てが行われるためです。

math.ceil関数｜正の無限大に近づく切り上げ

mathライブラリの「ceil関数」を使うと、正の無限大に近づく切り捨てができます。値の符号に関わらず、値が大きくなる方向に切り捨てが行われることが特徴です。

//サンプルプログラム

# coding: Shift-JIS

# mathライブラリを使用する
import math

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「math.ceil関数」で切り上げる
# この方法では「正の無限大に近づく切り上げ」が行われる
r1 = math.ceil(f1)
r2 = math.ceil(f2)
r3 = math.ceil(f3)
r4 = math.ceil(f4)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

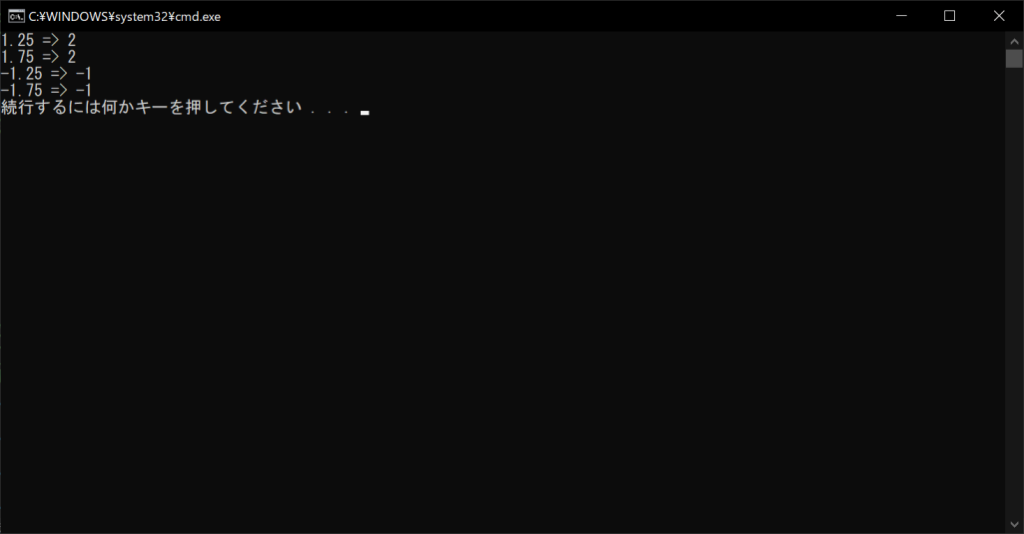
上記のように、「-1.25」や「-1.75」の切り上げ結果が「-1」になります。これは、正の無限大に近づく切り上げが行われることが理由で、一般的なイメージの切り上げに近いといえるでしょう。

quantize関数のROUND_CEILINGモード｜正の無限大に近づく切り上げ

quantize関数を「ROUND_CEILING」モードで使用すると、正の無限大に近づく切り上げができます。

//サンプルプログラム

# coding: Shift-JIS

# decimalライブラリを使用する
from decimal import Decimal, ROUND_CEILING

# 4つの浮動小数点数を定義する
f1 = 1.25
f2 = 1.75
f3 = -1.25
f4 = -1.75

# それぞれを「quantize関数」で切り上げる
# この方法では「正の無限大に近づく切り上げ」が行われる
r1 = Decimal(f1).quantize(Decimal("0"), rounding = ROUND_CEILING)
r2 = Decimal(f2).quantize(Decimal("0"), rounding = ROUND_CEILING)
r3 = Decimal(f3).quantize(Decimal("0"), rounding = ROUND_CEILING)
r4 = Decimal(f4).quantize(Decimal("0"), rounding = ROUND_CEILING)

# 処理結果を表示する
print(f"{f1} => {r1}")
print(f"{f2} => {r2}")
print(f"{f3} => {r3}")
print(f"{f4} => {r4}")

//実行結果

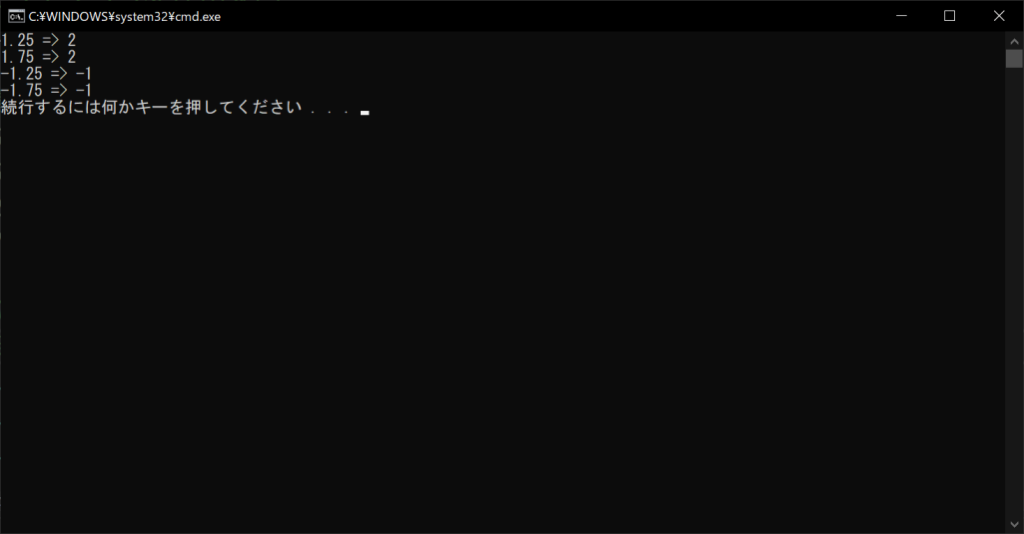
実行結果は「math.ceil関数」と同じです。いずれの場合も、元より値が大きくなる方向に、切り上げが行われます。

結論：Pythonの四捨五入には「quantize関数」がおすすめ

Pythonで四捨五入を行う際は、処理の方法と精度に注意が必要です。組み込み関数の「round」と「format」は、いずれも「銀行家の丸め」が行われるため、値によっては正確な四捨五入ができません。一方で、decimalライブラリの「quantize」は、正確な精度で四捨五入ができます。

今回ご紹介したように、自作関数も正しい四捨五入を行うことが可能です。しかし、正確な演算結果が保証されている公式関数であることや、切り捨て・切り上げにも簡単に対応できることなどから、quantize関数を使うのが一番の選択肢だといえます。Pythonの四捨五入の関数・メソッドを活用して、さまざまな処理を行ってみましょう。